One of my Pre-Cal students asked me a few days ago if the Law of Sines was hard to prove. I told him I'd write up a proof here. I also made my Pre-Cal class work through the proof themselves. I'll share their train of reasoning here.

First, we stated the Law of Sines:

in triangle ABC, a/sinA = b/sinB = c/sincC.

They quickly recognized that we need a diagram to work from. So we drew something like the diagram to the right.

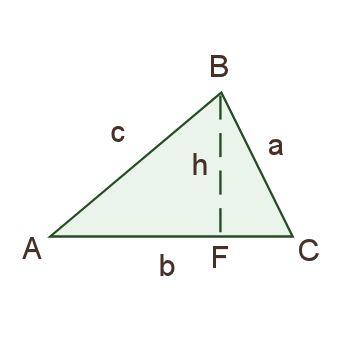
Then one of the students said, "Maybe we should draw in an altitude." Thus we had the following diagram. Their choice to label that new point F was somewhat random, I think, but I liked it, because F can stand for "foot" of the altitude.

After puzzling over their diagram for a bit, someone suggested setting up an equation involving the sine function and triangle ABF, and after a bit more thinking, a second equation involving the sine function and triangle CBF:

sinA = h/c; sinC = h/a.

They then did one of their favorite algebraic steps: multiplying both sides of an equation by a denominator in order to get rid of fractions (they don't like fractions, so they're always happy to get rid of them):

csinA = h; asinC = h.

A little substitution gives csinA = asinC. They then chose to divide both sides of this equation by sinAsinC, which gives:

c/sinC = a/sinA.

At this point, someone said, "Well we can just do this all over again with another side." Sure enough, if you drew an altitude to a different side, you'd get b/sinB = c/sinC (or b/sinB = a/sinA, depending on which altitude you drew).

Thus, a/sinA = b/sinB = c/sinC, and the Law of Sines is proved. Nice teamwork, class!