B.R. asks, "Can you explain what mechanical advantage is?"

Hi B.R., I'll give it a shot. Not knowing how much Physics background you have, I'll try to explain it in simple terms.

First of all, I'd like you to consider the following arrangement, which is a person pulling on a rope, which runs over a pulley, and down to an object with a weight of 400 Newtons (that's about 90 pounds, if you're used to using English units).

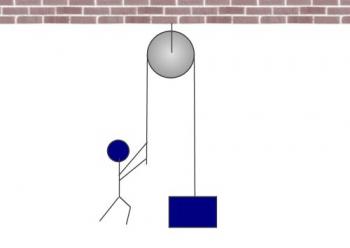
Now, when we talk about someone pulling on something, we're using the concept of a force.  Forces are measured in Newtons (or pounds). If the object has a weight of 400 Newtons, that means the person holding the rope has to pull with a force of 400 Newtons in order to keep the object from speeding up or slowing down. If he pulled with a force greater than 400 Newtons, the object would begin accelerating upward. If he pulled with a force less than 400 Newtons, the object would begin to accelerate downward.

This system has a mechanical advantage of 1. This means that on one end, the person applies a force that is equal to the force at the other end of the system. 400 / 400 = 1.

So let's take our pulley system and make it just a little more complicated. Here I've put a second pulley at the bottom, and attached the rope to the ceiling. The object hangs from the lower pulley. 

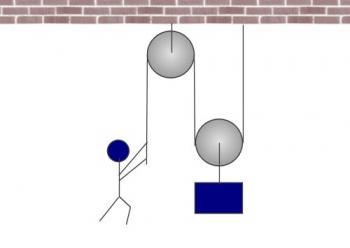
Now, one of the things that's important to understand is that if the man pulls with a force of 400 Newtons, there is tension in the rope, and the tension is the same everywhere along the rope. That tension is also measured in Newtons, and it is 400 Newtons. But here's where it gets interesting. Look at that lower pulley (that the object is hanging off). What is the tension in the rope to the left of the pulley? 400 N, right? What is the tension in the rope to the right of the pulley? It's also 400 Newtons. This gives a total of 400 + 400 = 800 Newtons. The upward force on the object is double the object's weight. This object is going to accelerate upward, even though in the first scenario, it would not have accelerated.

So if the man pulls with a force of 400 N, the output force is 800 N. The mechanical advantage is 800 / 400 = 2.

Incidentally, this means that the man could hold up an 800 Newton weight by applying a 400 Newton force. That's pretty impressive!

You could add more pulleys to the system, as shown here:

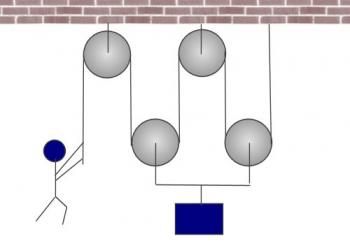
In this case, if the man is pulling with a force of 400 N, that means that there is 400 N of tension all through the rope, and so each of the lower pulleys has an upward force of 800 N, which means that the object (which is being supported from those two pulleys) has an upward force of 1600 N applied!

So the mechanical advantage is: 1600 / 400 = 4.

It seems like this is a win-win situation; you get better results by adding more and more pulleys. So why not add five hundred pulleys? If you did, you could hold up a 400 Newton object by applying a tiny, tiny force (less than 1 Newton!). So is it really a win-win situation? Not exactly. You see, there's a tradeoff for mechanical advantage. The tradeoff is the distance you pull the object. Take a look at the first diagram. If the man pulls the rope down 1 meter, the object will rise 1 meter. 

But what about the second diagram? What will happen there? Well, if the man pulls the rope down 1 meter, that meter is evenly distributed on either side of the lower pulley. Which means that pulley will only rise 0.5 meters. And therefore, if he pulls down a meter, the object only rises half a meter.

What about the third diagram? In that scenario, if the man pulls the rope downward 1 meter, that meter gets evenly distributed among four sections of the rope (one on either side of the two lower pulleys). In other words, the object only moves 0.25 meters.

So, if you had 500 pulleys, you'd be in the very interesting situation that you could easily lift a 400 Newton object, but it would take you a long time to do it; for every meter you pulled the rope down, the object would only move 2 millimeters!

There are many other kinds of machines: screws, wedges, levers, axle-and-wheels, and inclined planes. For every machine, there's a tradeoff; you can make the work easier, but in doing so, you end up extending that effort over a longer distance. An inclined plane is another easy one to picture. Imagine trying to lift a grand piano 1 meter straight off the ground. Can't do it, right? But if I made a long ramp, you could push the piano up. Much easier than lifting, but the tradeoff is that you have to push it a whole lot more than 1 meter!