Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Carol from South Paris asks, "After parentheses and exponents, order of operation is Multiply or Divide before Add and Subtract, then go left to right....but I'm puzzled about this one: 60 divided by symbol 5 (7 - 5). Is the answer 24 or 6? Thank you."
Hi Carol, I know exactly what you're talking about; I've been seeing this (and variations on it) cropping up on Facebook regularly in the last few days. It's funny how these things go in streaks. First it's problems about fruits and flower petals, and then people get tired of those, and it's back to order-of-operations again! Here's what the meme looks like, to help those who haven't seen it.

There are two common answers to this problem, and I show both ways of evaluating it below:
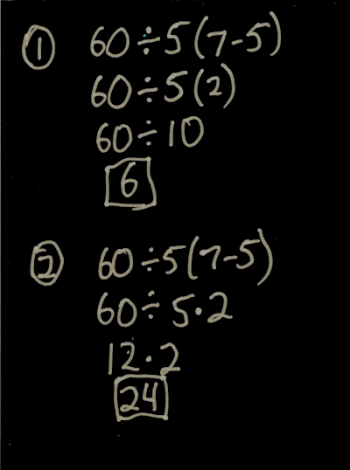
Why do people come to two different answers? And which one is correct?
There are two issues that lead to the confusion. The first is that when you first learned PEMDAS (or BODMAS, or whatever you called Order of Operations), you probably had not learned about the juxtaposition of parentheses with numbers and variables - if you saw this problem as a child, you probably saw it like this: 60 ÷ 5 x (7 - 5). That problem is entirely unambiguous. The correct order was to do the subtraction inside the parentheses first, then the division, and then the multiplication, giving you an answer of 24.
When you learned Algebra (or Pre-Algebra) you started using juxtaposition of parentheses with numbers, variables, and other parentheses to represent multiplication: 5(x + 1), x(x + 1), (x + 1)(x + 2). In each case, those can be thought of as: 5 · (x + 1), x · (x + 1), and (x + 1) · (x + 2). BUT...even though they "mean the same thing" you became trained, through usage, to treat the juxtaposed parentheses as an inviolable grouping. the 5 and the (x + 1) go together like peanut butter an jelly. This makes you, the algebra student, want to do the first evaluation method.
In PEMDAS we say that we do parentheses first. But what does that mean? Does it mean "Do what's inside the parentheses first," Or does it mean "Do what's inside and then combine the result with whatever the parentheses are juxtaposed with."? If you can't answer that question, you can't answer the meme.
What's the other issue here? The other issue is the fact that the operation symbol before the juxtaposed parentheses is a division symbol. If you stop to think about it, there wouldn't be an issue if it was multiplication, addition or subtraction. The problem would not have confused anyone if it had been 60 - 5(7 - 5) or 60 + 5(7 - 5).
This actually came up in my Algebra One class yesterday; we were discussing operation symbols, and I told them that in our algebra class, we would almost never use the division symbol used in this problem. Instead, we would use a vinculum (a horizontal fraction bar) to represent division.
Using a fraction bar removes the ambiguity from this problem, because if you use a fraction bar, you must make a choice in writing it out, as shown below.
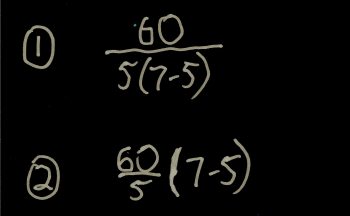
Okay, sure; we can make it unambiguous by changing our notation. But...who is right?
That question is a little tougher. You can find respected math websites and math video bloggers who come down on either side of the issue. And everyone tends to be emphatic that their interpretation is absolutely 100% correct. But that's not the worst of it; Texas Instruments made two different calculators (TI82 and TI83) that would evaluate this differently; one would give 6 as the answer, and the other would give 24.
For this reason (and I think it's a sufficient reason) I won't come down on one side or the other. Because if I told you that the first way was right, someday you'll be using the calculator that evaluates using the second method, or vice-versa. Until all our software consistently evaluates these things the same way (or refuses to evaluate them *), it's not safe to adamantly insist on one or the other. Instead, I tell my students, "If you're doing something like this on a calculator, always put in parentheses to clarify the meaning." But the reality is, this never comes up in my math classes, because we use the vinculum instead of the division symbol. You should do the same.
* People post screenshots of their desktop calculator (Windows) evaluating this to 24, but they never stop to think that they're actually changing the symbolic representation of the problem, because the Windows calculator refuses to do juxtaposition - it requires the use of a multiplication symbol. And since this problem is really all about symbolic representation, you cheated when you did that!
Professor Puzzler's brother, who is also a math teacher, and a coach of math teachers, adds the following advice that he gives his students:
- Estimate your answer first.
- Make sure you know how your calculator works on order of operations.

