Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Carol from South Paris asks, "After parentheses and exponents, order of operation is Multiply or Divide before Add and Subtract, then go left to right....but I'm puzzled about this one: 60 divided by symbol 5 (7 - 5). Is the answer 24 or 6? Thank you."
Hi Carol, I know exactly what you're talking about; I've been seeing this (and variations on it) cropping up on Facebook regularly in the last few days. It's funny how these things go in streaks. First it's problems about fruits and flower petals, and then people get tired of those, and it's back to order-of-operations again! Here's what the meme looks like, to help those who haven't seen it.

There are two common answers to this problem, and I show both ways of evaluating it below:
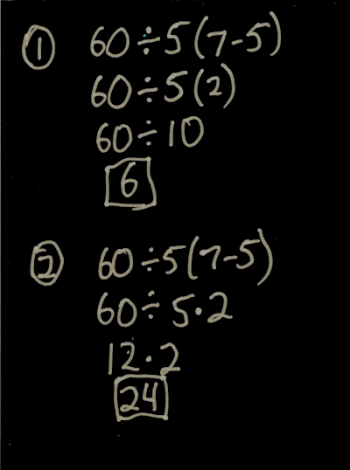
Why do people come to two different answers? And which one is correct?
There are two issues that lead to the confusion. The first is that when you first learned PEMDAS (or BODMAS, or whatever you called Order of Operations), you probably had not learned about the juxtaposition of parentheses with numbers and variables - if you saw this problem as a child, you probably saw it like this: 60 ÷ 5 x (7 - 5). That problem is entirely unambiguous. The correct order was to do the subtraction inside the parentheses first, then the division, and then the multiplication, giving you an answer of 24.
When you learned Algebra (or Pre-Algebra) you started using juxtaposition of parentheses with numbers, variables, and other parentheses to represent multiplication: 5(x + 1), x(x + 1), (x + 1)(x + 2). In each case, those can be thought of as: 5 · (x + 1), x · (x + 1), and (x + 1) · (x + 2). BUT...even though they "mean the same thing" you became trained, through usage, to treat the juxtaposed parentheses as an inviolable grouping. the 5 and the (x + 1) go together like peanut butter an jelly. This makes you, the algebra student, want to do the first evaluation method.
In PEMDAS we say that we do parentheses first. But what does that mean? Does it mean "Do what's inside the parentheses first," Or does it mean "Do what's inside and then combine the result with whatever the parentheses are juxtaposed with."? If you can't answer that question, you can't answer the meme.
What's the other issue here? The other issue is the fact that the operation symbol before the juxtaposed parentheses is a division symbol. If you stop to think about it, there wouldn't be an issue if it was multiplication, addition or subtraction. The problem would not have confused anyone if it had been 60 - 5(7 - 5) or 60 + 5(7 - 5).
This actually came up in my Algebra One class yesterday; we were discussing operation symbols, and I told them that in our algebra class, we would almost never use the division symbol used in this problem. Instead, we would use a vinculum (a horizontal fraction bar) to represent division.
Using a fraction bar removes the ambiguity from this problem, because if you use a fraction bar, you must make a choice in writing it out, as shown below.
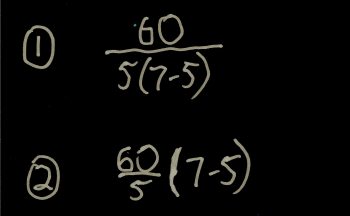
Okay, sure; we can make it unambiguous by changing our notation. But...who is right?
That question is a little tougher. You can find respected math websites and math video bloggers who come down on either side of the issue. And everyone tends to be emphatic that their interpretation is absolutely 100% correct. But that's not the worst of it; Texas Instruments made two different calculators (TI82 and TI83) that would evaluate this differently; one would give 6 as the answer, and the other would give 24.
For this reason (and I think it's a sufficient reason) I won't come down on one side or the other. Because if I told you that the first way was right, someday you'll be using the calculator that evaluates using the second method, or vice-versa. Until all our software consistently evaluates these things the same way (or refuses to evaluate them *), it's not safe to adamantly insist on one or the other. Instead, I tell my students, "If you're doing something like this on a calculator, always put in parentheses to clarify the meaning." But the reality is, this never comes up in my math classes, because we use the vinculum instead of the division symbol. You should do the same.
* People post screenshots of their desktop calculator (Windows) evaluating this to 24, but they never stop to think that they're actually changing the symbolic representation of the problem, because the Windows calculator refuses to do juxtaposition - it requires the use of a multiplication symbol. And since this problem is really all about symbolic representation, you cheated when you did that!
Professor Puzzler's brother, who is also a math teacher, and a coach of math teachers, adds the following advice that he gives his students:
- Estimate your answer first.
- Make sure you know how your calculator works on order of operations.
Everett, from Illinois, writes, "I was born in 1937 in Southern Illinois, Franklin County. We were not taught PEMDAS in school. When did they start teaching this order of operations. Is it taught all over the state now?"
Hi Everett, since the beginning of people writing down mathematical ideas, mathematicians have had to develop conventions for indicating the meaning of expressions on paper. Those rules have not always been consistent. For instance, as a precursor to parentheses, some mathematicians used to write expressions with a horizontal bar over the top to indicate that things should be grouped.
Consider the expressions 7 x 2 + 3. This looks like it should be 14 + 3 = 17. But if the author of a text wanted the addition to be done first, he would write:
_____
7 x 2 + 3
Typographically, this was cumbersome, and eventually led to the idea that parentheses could be used, and would be simpler to write. This was first suggested in the early 1600s, so it was in vogue as a mathematical ordering notation long before you were born.
Exponents were first used much earlier than the 1600s, but there was no "official" way to write them. Some used Roman Numerals for exponents, some wrote a number after a variable, but not raised (thus, 3x meant 3 times x, but x3 meant x to the third power). It was probably Rene Descartes who made the raised notation popular, and it became the standard. Descartes was doing this in the mid 1600s (not too long after the parentheses started becoming popular). And because of the way it was written, outside the normal baseline of the equation, it had an implicit ordering to it. You would never see the following expression:
23 + 1
and interpret it as though the 3 and the 1 should be combined first, and then 2 raised to the 4th power.
So there you have the first two elements of PEMDAS - parentheses and exponents - that have been implicitly understood since the 1600s.
As for multiplication and division coming before addition and subtraction, I'm not clear on exactly when these became part of the standard ordering notation. However, if you took an Algebra class in high school, you used this ordering of operations, even if no one taught you a name for what you were doing. Consider the following examples:
Example One: Multiplication before Addition
5 + 3x
If multiplication was not evaluated before addition, this would be evaluated (as some of my Algebra students like to do) as:
5 + 3x = 5 + 3 · x = (5 + 3)x = 8x.
The ordering of multiplication and addition was implictly given in the rules for how we can manipulate terms in an expression.
Example Two: Division before Addition
5 + 1/x
If division was not evaluated before addition, this would be evaluated as (5 + 1)/x or 6/x. Again, this order of operations was inherent in the rules for manipulating terms of an algebraic expression.
Which brings me to the answer to your question. First, I do think it's possible that you were never taught PEMDAS as a specific notational convention, but all the rules of the PEMDAS mnemonic were in existence long before you were born. Secondly, even if you weren't taught it specifically, you still used it when you did Algebra, and if you passed your algebra class, then you were doing it correctly! Finally, yes, PEMDAS (or BODMAS*) is taught consistently worldwide. There are still arguments that arise about some ambiguous notations (you may have read one or more posts about those), but PEMDAS is the standard convention for interpreting expressions worldwide.
* BODMAS is used (I believe) in Britain, and perhaps other places as well. B = Brackets, O = Order. Brackets are parentheses, of course, and Order is the word used for Exponents, so even though it looks different, it's the same convention.
Several months ago, Professor Puzzler wrote a blog post about the math problem "three over two x" (3/2x) and how it should be interpreted. The answer was: that's not a math problem; it's a typographical error, because fractions written with a diagonal bar, by typographical standards, should be written with the numerator a superscript, and the denominator a subscript, making it obvious whether the x is a part of the denominator, or separate from the fraction altogether.
A similar question has cropped up, and someone asked the Professor about how to interpret it: what is the answer when you perform the following operations:
6 ÷ 2(1 + 2)
This is another one of those facebook memes that people love to argue endlessly about. The primary arguments go as follows:
Argument #1
Do the parentheses first, giving you 6 ÷ 2 x 3. Now do the multiplication, giving: 6 ÷ 6. Now do the division and the answer is 1.
Argument #2
Do the parentheses first, giving you 6 ÷ 2 x 3. Now do the division, giving: 3 x 3. Now do the multiplication and the answer is 9.
Argument #3
Do the parentheses first, giving you 6 ÷ 2(3). Now do the parentheses (again), giving: 6 ÷ 6. Now do the division and the answer is 1.
Which of these arguments are valid?
Argument #1 is invalid, because once you're left with just division and multiplication, you do them from left to right. Multiplication does not take precedence over division! If you used argument #1, you should review BODMAS (PEMDAS).
Argument #2 is an acceptable argument. Here you're doing the multiplication and division from left to right, as required.
Argument #3 is also invalid, because "doing parentheses" means evaluating what's inside the parentheses, not combining them with things outside the parentheses.
Does that mean the answer is unequivocally 9? Or is there another argument to be made?
I'm going to stir the pot a little and suggest that there is another argument you could make.
Argument #4
BODMAS (PEMDAS) is a set of rules that is designed to tell us what to do with specific arithmetic operation graphemes*, and if we represent an arithmetic operation with a grapheme outside the set of graphemes, all bets are off.
* A grapheme is a visual, symbolic representation of something. For example, "A", "1", "÷" are all graphemes.
If you don't believe that using different graphemes can alter the order in which we do the problem, consider the following. Division can be represented by the symbol "÷" or by a vinculum (a horizontal fraction bar). With that in mind, are the following equivalent expressions?
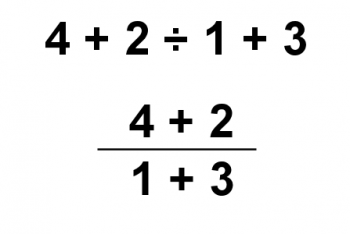
The answer is: of course they're not the same! The top expression is evaluated with 2 ÷ 1 calculated first, and then 4 + 2 + 3 = 9.
In the second expression, we evaluate the numerator and denominator first, giving 6 ÷ 4. Which gives 3/2 as the answer.
But they are both graphical representations of division! So why does the order of operations change? I tell my students that the vinculum is a "grouping symbol." In other words, it has implied parentheses. If you wanted to write it without the vinculum, you would have to add parentheses to the expression:
(4 + 2) ÷ (1 + 3)
Thus, even though the vinculum and "÷" are both division symbols, order of operations does not apply to them in exactly the same way.
In the same manner, one could argue that multiplication written with a different grapheme (in this case, the grapheme would be no grapheme at all) doesn't need to be interpreted in exactly the same way as multiplication written with the standard "x" grapheme. You could argue that in the same way that a vinculum as the division grapheme introduces implied parentheses into the problem, an empty grapheme for multiplication also introduces an implied grouping. In other words, 2(2 + 1) is actually an implied group: [2(2 + 1)]. This would change the answer to the original problem to 1 instead of 9.
And I would be hard pressed to provide a compelling argument against your interpretation, since I just got done telling you that a vinculum introduces an implied grouping!
Which leads us to the point I wanted to make from the beginning:
This is one of the reasons why, once we hit Algebra, we avoid using the ÷ grapheme for division. We almost entirely use a vinculum for division. Partly, that's because it allows us to be more compact in writing problems. But also because it becomes an implied grouping for division (allowing us to skip writing parentheses all over the place) AND it also avoids any chance of ambiguity that might arise from the question of how we write our multiplication. If a no-grapheme multiplication occurs under the vinculum, then it already has an implied grouping which it receives from the vinculum!
Seventh grader omarion, from Georgia, asks, "Why can the “M” and the “D” switch places without changing the order of operations?"
Hi omarion! You've hit on one of the things that is most confusing about Order of Operations. It shouldn't be confusing, but I think sometimes teachers either don't teach Order of Operations correctly, or they teach it correctly but unclearly or incompletely.
You've probably been taught PEMDAS, which stands for: parentheses, exponents, multiplication, division, addition, and subtraction. And you may have been told you can remember PEMDAS by remembering the silly phrase, "Please Exuse My Dear Aunt Sally," in which the first letter of each word corresponds to the first letter of each word in the PEMDAS list.
If that's what you were taught, it's not wrong...exactly...but it's also not complete.
So let me tell it to you a different way.
- Grouping symbols (like parentheses) are most important.
- Exponents are the next most important operation.
- Multiplication and Division are equally important, and they are next after exponents.
- Addition and Subtraction are equally important, and they are after multiplication and division.
- If you have operations that are equally important, you do them in the order that you read the expression (from left to right!)
Multiplication and Division are equally important, so you need to do them from left to right. Similarly, you do addition and subtraction from left to right. So let's try an example problem.
3 · (3 + 5) - 2 ÷ (33 - 52) + 3 · 2
To help you understand how we do this, we're going to simplify it one step at a time. Ready?
Order of operations says that we do parentheses first. But there are two sets of parentheses, right? Which one has higher priority? That's where our last rule comes into play. The one on the left comes first. So first we evaluate the first set of parentheses:
3 · 8 - 2 ÷ (33 - 52) + 3 · 2
Then we evaulate the only other set of parentheses. But wait! the second set of parentheses has multiple operations! Two exponents, and one division! So we tackle this in the following order: first exponent, second exponent, then subtraction. Here it is:
3 · 8 - 2 ÷ (27 - 52) + 3 · 2
3 · 8 - 2 ÷ (27 - 25) + 3 · 2
3 · 8 - 2 ÷ 2 + 3 · 2
So what's next? Multiplication and division. Which is more important? Neither! They're equally important. So we do them from left to right. So follow each step, and see which operation I evaluate in each step.
24 - 2 ÷ 2 + 3 · 2
24 - 1 + 3 · 2
24 - 1 + 6
Now we only have addition and subtraction. Which is more important? Neither! So we go from left to right, which means doing the subtraction, and then the addition:
23 + 6
29
So, in answer to your question, why can we switch the "M" and the "D" in PEMDAS? It's because neither M nor D is more important than the other. Similarly, neither A nor S is more important than the other. So actually, if I wanted, instead of talking about PEMDAS, I suppose I could talk about...
PEDMSA!
Which, of course, stands for...
Professional Educators Delight Many Students of Algebra!
Today's post is about a picture that has been mystifying and frustrating people. Frustrating because it seems so blatantly and completely wrong. Mystifying because people in the know just smile knowingly as though it's a joke.
Some jokes need to be explained, so here's the picture:

It seems quite clear, doesn't it? PEMDAS gives us our order of operations. We evaluated 85 + 65 first: 85 + 65 = 150.
So now we have 25 - 55 + 150, which should be evaluated in order from left to right: 25 - 55 = -30, and -30 + 150 = 120.
So how in the world did they get 5?
The answer is: they didn't get 5. They got 5!
You see, this is one of those horrible times when mathematics hijacks innocent punctuation marks and forces them into hard labor for nefarious, non-grammatical purposes.
The exclamation mark is used in mathematics not to epxress excitement or astonishment, but to indicate that we are calculating the factorial of a number.
What's a factorial? A factorial is what you get when you multiply all the integers between 1 and some number. For example, 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720.
So before we declare this image bogus and invalid, we probably should check to find out what 5! equals.
5! = 5 x 4 x 3 x 2 x 1 = 120.
Oh! (And I'm using that exclamation mark to indicate astonishment) it really does equal 5!
And if I'm truly astonished, I might say that it equals 5!!
Except someone might get hoodwinked into thinking I meant 120!, which is about 6.8 x 10198. That's not what I meant. I promise. I'm just that excited!


