I had a student ask today why Cramer's Rule works. That's the sort of question I love, but we didn't have time in class to work through it, so I thought I'd post the exploration of the question here. We'll consider the case of a system of two equations in two unknowns.

Cramer's Rule says that if you have a system written as follows:

ax + cy = e
bx + dy = f

Then we can find the values of x and y by evaluating the following determinants.

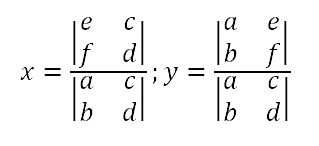
In case you're not familiar with determinants, we find the value of a 2 x 2 determinant by multiplying the numbers along the primary diagonal (top-left to bottom-right) and then subtracting the product of the other diagonal. Thus, this could be rewritten as follows:

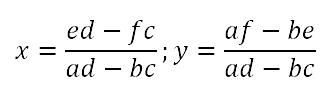
So that's the form we're going to consider. Ideally, we'd like to show that given the system we started with, the solutions can be written in the form directly above.

If you were solving a system of equations with numeric coefficients, you might find the least common multiple of the coefficients of x, and then figure out what you need to multiply each equation by in order to get those coefficients to cancel. Unfortunately, we don't have numeric coefficients, but we can still do this process. What is the LCM of a and b? Why, it's the product of a and b! So we'll multiply the first equation by b, and the second equation by -a:

 bax + bcy =  be
-bax - ady = -af

Adding these two equations gives us

bcy - ady = be - af 
y(bc - ad) = be - af    (factor out y)
y = (be - af)/(bc - ad)    (divide both sides by (bc + ad)

Now, that doesn't exacly match the result we expected, but if we multiply the top and the bottom by -1, we get:

y = (af - be)/(ad - bc)

That's only half of the problem, of course; we've shown that the "y" formula works; now we just need to show that the "x" formula works.

And you know what? We'd show it exactly the same way, except we'd start by eliminating y instead of x. I'll leave that to you to work out on your own. And, of course, once you've finished that, you can develop your own proof for systems of three equations in three unknowns!