"If the two triangles shown are similar, find the value of d/c. I know the answer is 5/6, but I don't know how to get it." ~Kimberly

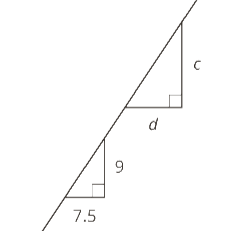
Good morning Kimberly. As we look at this question, I'd like to point out that it does violate one of our standard rules of geometry - which is that we never assume the diagrams are drawn to scale. The problem writer clearly intends for you to assume that the lines which appear to be horizontal really are horizontal, and the ones that appear to be vertical really are vertical. If you make that assumption, then you can conclude that the side of length 7.5 corresponds to the side of length d, and the side of length 9 corresponds to the side of length c. So we'll go with that assumption.

Since the triangles are similar, and we "know" which sides are corresponding, we can set up a ratio:

7.5/d = 9/c.

This does not give us what we want (d/c). However, we can rearrange that with just a couple steps to obtain the desired result. First multiply both sides by d, to get it in the numerator:

d(7.5/d) = d(9/c)
7.5 = 9d/c

Now divide both sides by 9:

7.5/9 = d/c

This is the ratio you want, except that it's not in simplest form. Multiply numerator and denominator by 2 in order to get rid of the decimal:

7.5/9 = 15/18 = 5/6.

And there's your answer. But I'm not quite done - I'd like to point out something that might be valuable to you. This problem shows us something very interesting that I often make use of when doing similar triangle problems.

We started with a ratio of corresponding sides, and when we were done, we ended with a very different ratio - the ratio of sides within a triangle.

Your standard rule is: The ratios of corresponding sides in two similar triangles are equal.

Our alternate version (which you can call the Kimberly Rule, if you want) is: The ratio of any two sides in a triangle is equal to the ratio of the corresponding sides in a second, similar triangle.

In other words, you could have started out with d/c = 7.5/9 instead of starting out with 7.5/d = 9/c.