Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Judah from Maine asks for an explanation of how to negate a compound statement.
We'll explore two possibilities. One is that the compound statement contains an "AND" and the other that it includes an "OR." Let's make up one statement for each possibility.
- It's snowing or it's raining
- Christmas is almost here, and the elves are hard at work.
To help you visualize these, I've made Venn Diagrams for each. Let's start with the weather example:
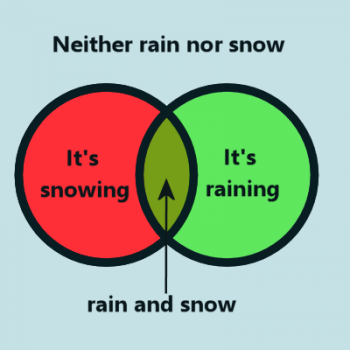
In this example, the red region represents the condition of snow, and the green region reporesents rain. Thus, the greenish-yellow region represents both rand and snow, and the blue region (outside the two circles) represents the condition that it is neither raining nor snowing. This covers all the possible conditions (that is - all the conditions we're concerned about here - there are, of course, other weather conditions like sleet, freezing drizzle, etc, but these are not our concern right now). The possible conditions are:
-
There is neither rain nor snow.
- There is snow, but not rain.
- There is rain, but not snow.
- There is both rain and snow.
Which of those four matches our initial condition? The statement "It's snowing or it's raining" is covered by the red, green, and greenish-yellow regions. That's regions 2, 3, and 4. Therefore, the the logical NOT of "It's snowing or it's raining" must contain everything except those three regions. Or, to put it more simply, it has to be only region 1 - neither rain nor snow.
So the negation of "It's snowing or it's raining" is "It's not snowing and it's not raining." Interesting, isn't it? When you negated an "or" you got an "and." Let's see what happens with our other example:
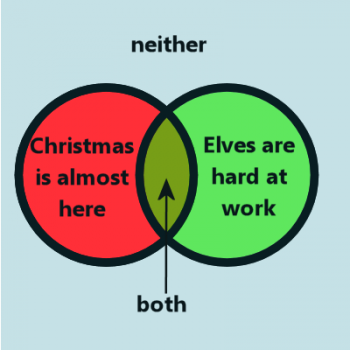
In this case, the red region represents Christmas being almost here, the green region is elves hard at work, and the greenish-yellow region is both Christmas is almost here and elves are hard at work. The light blue region represents neither of the statements being true.
So which region(s) represent our original statement? "Christmas is almost here, and the elves are hard at work." This is only covered by the overlapping greenish-yellow region.
So if we want to negate this one, we need to figure out a way of expressing everything except the greenish-yellow region. It's tempting to say that the negative of the statement is "Christmas is not almost here, and elves are not hard at work," but that is only the blue region; it doesn't include the red or the green. So instead, we need to say "Christmas is not almost here, or elves are not hard at work." Using an "or" instead of "and" allows us to include all the regions in the Venn diagram.
So our general rule of thumb is, if we're trying to negate a compound statement, we need to make sure that the original statement and it's negation cover every single region of the diagram, without any overlap.
If you've got that, you can go a little crazy with compound statements:
(It's raining and Christmas is almost here) or (it's snowing or the elves are hard at work).
Can you negate that statement?
Question
Hi Professor Puzzler, I was wondering if you could explain what an axiom is?
Katie M, Grade 11
South Dakota
Answer
Hi Katie,
Well, I'm guessing that you're taking a Geometry class, because that's when many students first see that term.
An axiom is something that you believe or accept to be true without having ever proven it. It is something that you consider to be "obviously true." You might not realize it, but your life is filled with axioms - things that have never been proven to you, but you believe anyway. I once asked a group of high school students to name some things they couldn't prove, but they were confident of anyway. Here were some of their answers:
- My parents love me.
- The sun will rise tomorrow.
- Gravity keeps me from falling out into space.
- There is a God.
- 1 + 1 = 2.
Why are axioms important? Because when you are proving something, there will always be fundamental building blocks of ideas that your proof is based on, and it's important to remember that the most fundamental building blocks are actually things you haven't proved at all.
In a way, an axiom is sort of like what the Bible says about faith: faith is the substance of things unseen.
Euclid had some axioms (or postulates), and one of his very important axioms was that if you have a line, and a point that's not on the line, there's only one line that goes through the point, and is parallel to the line. That might seem obvious, but some other mathemeticians like Lobachevsky, Riemman, and Gauss had some different ideas, and their notions of geometry turned out to be very different from Euclid's.
The assumptions you start with can drastically change your results!
In modern usage, the "obviously true" concept is not how axioms are always viewed; in another sense, we could view an axiom as simply a "rule of the game" in mathematics. In other words, mathematicians might say, "Let's start from assumption X, and see what sort of mathematics we develop!" The assumption, or axiom they begin with may not be something that's "obviously true," but often valuable results come from such game playing.
Thanks for writing,
Professor Puzzler

