Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!

Merry Christmas! A couple years ago I mentioned here that someday I would post instructions and templates for creating various ornaments out of cardstock and/or photo paper. Considering we're just days away from Christmas, some parents may be looking for fun activities to do with their children to pass the time on their way to the most anticipated day of the year, so I have put those plans online at last!
We have a whole "Paper Craft" section now, and it includes instructions for several ornaments like the one shown here. Note that the templates are blank (without images). This allows you to add your own clipart (in case you wanted a Santa-themed ornament, or a snow-themed ornament instead of a religious-themed ornament).
And you don't need clipart at all; I printed out some blank ones and my kids loved drawing their own pictures on them.

We have the following ornament templates/instructions:
The cube is a good size to put on a tree; the other two are too large for a tree. The dodecahedron was designed as a table-top ornament, and the icosahedron as an ornament to hang from the ceiling or doorway frame.
In addition to the ornaments, there are several tutorials, in case you are interested in designing your own projects, such as the partially complete cathedral shown here.
Happy crafting, and Merry Christmas!
From Amber: "I'm trying to figure out the angle of a set of stairs using a scalene triangle basically you have a 90 degree angle one side is 8 feet and one is 3.5 feet what would be the slope or the angle of the third side"
Hi Amber. You didn't state in your question whether 8 feet is the horizontal length of the staircase and 3.5 feet the height? Or perhaps 8 is the length along the slope of the staircase? Of course, that makes a difference, so I'll help you work it out both ways.
First, as you pointed out, you have a right triangle. If the 8 and 3.5 are the legs of the triangle, that's all you need.
However, if 8 is the hypotenuse, you need to use the Pythagorean Theorem to find the missing side length: x2 = 82 - 3.52. Which leads to x = 7.2 (approximately)
There are two basic rules that you need to know. The first rule is that the slope is "rise over run." In other words, it's the amount that the staircase rises divided by the amount the staircase goes horizontally. So if the staircase is 8 feet horizontally and 3.5 feet vertically, the slope is 3.5 / 8 = 0.4375. On the other hand, if the horizontal length is 7.2, the slope is 3.5 / 7.2 = 0.4861.
Okay, so now you need the second rule, which is that the slope is the slope is the same as the tangent of the angle. Or, to put it a little differently, the angle is the inverse tangent of the slope.
You probably know how to do trig functions on your calculator, but in case you don't, on most calculators, you'll get the inverse tangent function by pressing "2nd" (or "Shift") and then the "TAN" button. So you'll press 2nd TAN 0.4375 = 23.6 degrees. Or, if we're using the second possibility, 2nd TAN 0.4861 = 25.9 degrees.
In either case, that's a fairly shallow angle for stairs; I think the "standard" (at least in the US) is closer to 30 degrees than 25 degrees.
Hopefully that helps out - thanks for asking!
Chanchal from Muktsar asks if we could prove that in a quadrilateral the sum of exterior angles is 360°.
Good morning, Chanchal. One of the challenges of doing proofs on this blog is, a proof is constructed from the building blocks of things we already know, stacked together to create something we don't already know, and since I don't know you, I don't know what building blocks (knowledge) you have that you can build from. So before I start talking through the proof, here are some of the building blocks I'm going to use - in case you don't already know these things:
- the sum of the interior angles in a triangle is 180°
- when two lines intersect, they form four angles that add to 360°.
- vertical angles are congruent (vertical angles are the angles across from each other formed by two intersecting lines)
Okay, with that as background, let's look at a diagram.
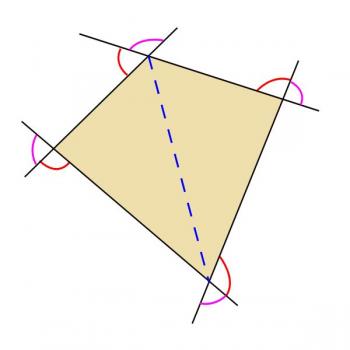
Now, my diagram is not just a quadrilateral - I've added some extra lines into it.
- The blue dashed line is a diagonal of the quadrilateral
- The sides of the quadrilateral have been extended to form exterior angles
- The purple arcs indicate angles which are opposite (vertical) to the interior angles of the quadrilateral
- The red arcs indicate the angles we're interested in.
Note that when we talk about the exterior angles of a quadrilateral, we're not talking about all the angles formed by the sides that lie outside the quadrilateral. We're not including the purple angles, and we're also not including the angles opposite the red ones. The exterior angles are all the angles "facing the same way" around the quadrilateral. That's not a very precise way of describing them, but hopefully you can see from my picture what I mean by that.
Okay, so how do we prove this? I'll give you two methods, and you can decide which one you like best. Ready?
Proof #1
- A quadrilateral can be divided into two triangles by a diagonal
- Each triangle has 180 degrees
- 180 x 2 = 360, so there are 360 degrees in the interior of a quadrilateral.
- Call these four angles a, b, c, and d. Then a + b + c + d = 360
- Each angle is supplementary to an exterior angle.
- Thus, the exterior angle measures are 180 - a, 180 - b, 180 - c, and 180 - d
- Adding these together gives (180 - a) + (180 - b) + (180 - c) + (180 - d) = 720 - (a + b + c + d)
- Since a + b + c + d = 360, this is equal to 720 - 360, which equals 360 degrees.
Proof #2
(Proof #2 starts out with some of the same steps as Proof #1)
- A quadrilateral can be divided into two triangles by a diagonal
- Each triangle has 180 degrees
- 180 x 2 = 360, so there are 360 degrees in the interior of a quadrilateral.
- Call these four angles a, b, c, and d. Then a + b + c + d = 360
- The intersecting lines at the four vertices form angles adding to 360 degrees
- Since there are four such sets of angles, their measures add to 360 x 4 = 1440 degrees.
- The purple angles from vertical pairs with the interior angles, so their measures are a, b, c, and d
- Thus, the sum of the red angles and their vertical counterparts is 1440 - (a + b + c + d) - (a + b + c + d) = 720 degrees
- Since vertical angles are congruent, we divide this sum in half to obtain the sum of the red angles: 720 / 2 = 360 degrees.
Incidentally, this proof can be extended to show that this is true not just for quadrilaterals, but for any polygon; the sum of the exterior angles is 360 degrees, regardless of the number of sides. Thanks for asking, Chanchal!
"If the two triangles shown are similar, find the value of d/c. I know the answer is 5/6, but I don't know how to get it." ~Kimberly
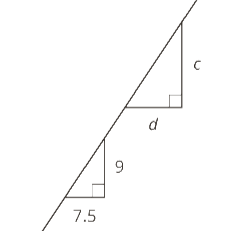
Good morning Kimberly. As we look at this question, I'd like to point out that it does violate one of our standard rules of geometry - which is that we never assume the diagrams are drawn to scale. The problem writer clearly intends for you to assume that the lines which appear to be horizontal really are horizontal, and the ones that appear to be vertical really are vertical. If you make that assumption, then you can conclude that the side of length 7.5 corresponds to the side of length d, and the side of length 9 corresponds to the side of length c. So we'll go with that assumption.
Since the triangles are similar, and we "know" which sides are corresponding, we can set up a ratio:
7.5/d = 9/c.
This does not give us what we want (d/c). However, we can rearrange that with just a couple steps to obtain the desired result. First multiply both sides by d, to get it in the numerator:
d(7.5/d) = d(9/c)
7.5 = 9d/c
Now divide both sides by 9:
7.5/9 = d/c
This is the ratio you want, except that it's not in simplest form. Multiply numerator and denominator by 2 in order to get rid of the decimal:
7.5/9 = 15/18 = 5/6.
And there's your answer. But I'm not quite done - I'd like to point out something that might be valuable to you. This problem shows us something very interesting that I often make use of when doing similar triangle problems.
We started with a ratio of corresponding sides, and when we were done, we ended with a very different ratio - the ratio of sides within a triangle.
Your standard rule is: The ratios of corresponding sides in two similar triangles are equal.
Our alternate version (which you can call the Kimberly Rule, if you want) is: The ratio of any two sides in a triangle is equal to the ratio of the corresponding sides in a second, similar triangle.
In other words, you could have started out with d/c = 7.5/9 instead of starting out with 7.5/d = 9/c.
"How do you add 8 cubic yards and 8 cubic feet?" ~Anon.
Since you're asking the question, you're probably deduced that you can't simply add 3 and 3 to get 6. If you did that, you'd then have the question of whether the units in the result are cubic yards or cubic feet. The simple rule is that you can't add two quantities which have different units.
If two units are the same type of unit (for example, they're both distances, or they're both times), then you can rewrite one of them so they have the same unit, and then you can add them.
In this case, both units are volumes, which is an amount of 3-dimensional space something takes up. We want to either convert 3 cubic yards into cubic feet, or we want to convert cubic feet into cubic yards. I'm going to convert cubic yards into cubic feet.
If you have 8 cubic yards, you can picture that as a cube. Conveniently, 8 = 23, so you can picture it as a cube that has a width of 2 yards, a height of 2 yards, and length of 2 yards. Length times width times height = 2 yards x 2 yards x 2 yards = 8 yards3.
But we know how to convert 2 yards into feet; there are 3 feet in a yard. So it turns out that our cube's dimensions are 6 feet by 6 feet by 6 feet. So Length times width times height = 6 x 6 x 6 = 216 feet3.
Now that we have written both units in cubic feet, we can add them: 216 feet3 + 8 feet3 = 224 cubic feet.
That answers your question, but we've really only touched the surface of converting units - you can find a more detailed study unit here: Conversions factors and unit conversions.

