The Professor Puzzler blog has been pretty quiet recently, so I'm breaking the monotony by asking myself a question.

Me: Professor Puzzler, what is a Double-Dactyl poem, and how do you write one?

Other Me: That's a great question! I hesitate to say that the Double-Dactyl is one of the silliest poetry forms in existence, but…well…it’s one of the silliest poetry forms in existence.

Let’s start with a Double-Dactyl example, and then we can dissect it to understand how the form works. This is a poem about Noah (yes, the guy with the ark).

Splishity splashity
Noah the Patriarch
Built a big boat out of
Gopher-wood trees

Finding some grace in the
Eyes of Jehovah, this
Antediluvian
Sailed o'er the seas

Before we get into the rules, what is a dactyl? A dactyl is a metrical foot which consists of one stressed syllable followed by two unstressed syllables. In other words, it sounds a bit like a waltz. OOOM-pah-pah OOOM-pah-pah. Okay, now let’s dive in.

1. There are two sets of four lines. These sets of four lines are called “quatrains.”
2. In each quatrain, the first three lines are each two dactyls. The last line of each quatrain is a single dactyl followed by one accented syllable (OOOM-pah-pah-OOOM)
3. The only rhymes we need are at the end of the two quatrains.
4. The first line must be nonsense words. Since they’re nonsense, they don’t have to have anything to do with the subject of the poem, but it can be fun – as I did in my Noah poem – to make them similar to real words that connect to the subject of the poem.
5. The second line must be a proper noun. This would most commonly be a person’s name (or name and title), but could also be a place, organization name, or even something like “U.S.S. Nautilus.” In the example above, NO-ah the PA-tri-arch has the accents on NO and PA, with the other syllables unaccented.
6. Somewhere in the poem – preferably in the second quatrain, and usually the sixth line of the poem (but the location is not a hard-and-fast rule), there must be a line that consists of a single six-syllable word that fits the dactyl rhythm. In the Noah poem, that word is “antediluvian” (which means “before the flood”).

There you have it – now you’re ready to write your own Double-Dactyl. On my YouTube channel (link: Doug's ventiloquism, music, and teaching) my puppets (yes, I’m a ventriloquist!) and I will posted a series of three Double-Dactyls. The third in the series is actually sung instead of recited; if you learn the tune, that may help you write your own Double-Dactyls!

Wiffity Woffity (a poem about a timberwolf and a dodo bird)

Axity Waxity (a poem about George Washington and a cherry tree)

Offity Scoffity (a poem about Alice in Wonderland)

Note that in my poems, my nonsense words all end in “-ity” but that is not a requirement; I just like the way it sounds. I guess I just got stuck in a nonsense rut.

Finally, if you’re interested in other kinds of poetry, one of my puppets shares his own rendition of Robert Burns’ “My Love Is Like a Red, Red Rose,” and several of my puppets have done limericks: Jeorge’s Limerick, Jeffrey’s Limerick, Professor Jameson’s Limerick, Doctor Jonas’ Limerick.

And for those who like Star Wars, be on the lookout for some Star Wars themed Double Dactyls late in 203!

Rosanna from Italy writes, "I'm an Italian student of English, dealing with learning literature. Introducing the Medieval ballad, after analysing Lord Randal, we're analysing Geordie, the English version. Our book text introduces the counting of stressed and unstressed syllables in medieval ballads but the answer seem to get me confused because it is said that there is a mixed of four and three stressed syllables lines without indicating the lines. Can you tell me what the lines are, what the stressed and unstressed syllables are and if we can specify if they are iambic or anapest feet? Thanks in advance, I really need your help!"

As I walk’d o’er London Bridge
One misty morning early
I overheard a fair pretty maid,
Was lamenting for her Geordie.

"O, my Geordie will be hang’d in a golden chain,
’tis not the chain of many,
He was born from King’s royal breed
And lost to a virtuous lady."

Go bridle me my milk-white steed,
Go bridle me my pony,
I will ride to London’s Court
To plead for the life of Geordie.

"O Geordie never stole nor cow, nor calf,
He never hurted any,
Stole sixteen of the King’s royal deer
And he sold them in Bohenny.

"Two pretty babes have I born,
The third lies in my body,
I’d freely part to them ev’ry one
If you’d spare the life of Geordie."

The judge look’d over his left shoulder,
He said, "Fair maid, I’m sorry,
So, fair maid, you must be gone,
For I cannot pardon Geordie."

O my Geordie will be hang’d in a golden chain,
’tis not the chain of many,
Stole sixteen of the King’s royal deer
And he sold them in Bohenny.

Hi Rosanna, you've got an especially interesting poem to decipher. Ballads are made challenging by the fact that they were originally intended to be sung rather than spoken. Song-writers often feel like they have more flexibility in their writing than poets who intend their poems to be spoken. The reason for this is that it's easier to cram extra syllables into a song; all you have to do is take a quarter note and change it into two eighth notes, and you've put an extra unaccented syllable between your accented syllables.

To see this illustrated, a good starting point is to find an audio recording of the ballad and listen to it. Here's one I found. The lyrics are not exactly the same as the copy you sent me, but they're fairly close. Geordie Ballad on YouTube.

One of the best lines to hear this "syllable cramming" that I mentioned above is the first line of the repeated chorus in the video:

"He never stole a cow, never stole a calf"

When you listen to that line, you can hear that the singer is really working to fit extra syllables in. In particular, "stole a" in the first half of the line and "never" in the second half are jammed together to make the line of music flow. If you focus your attention on what syllables get accented here, what you'll hear is:

'he NEV-er stole a COW, nev-er STOLE a CALF"

Interesting, isn't it, that the first time the word "never" shows up it has an accented syllable, but the second time it shows up, the entire word gets jammed into the space between two accented syllables. This sort of thing makes poetry both interesting and challenging!

If I were going to break this down by accented and unaccented syllables, I might replace each unaccented syllable by a lower case "x" and each accented by an exclamation mark. It would look like this:

x ! x x x ! x x ! x !.

This doesn't seem terribly helpful; the number of unaccented syllables does not stay consistent throughout the line. However, at the very least we can tell that there are four accented syllables in this line. Now let's look at the next line:

"He never murdered any."

This one is much more straightforward, and if you just simply read it aloud, you would hopefully hear the natural rhythm of it:

"he NEV-er MUR-dered AN-y"

So this one is: x ! x ! x ! x, which has three accented syllables.

The next line is "STOLE six-TEEN of the KING'S ro-yal DEER" , which is: ! x ! x x ! x x !. 

And finally: "and he SOLD them IN bo-HENN-ey" or: x x ! x ! x ! x.

Let's put it all together to make an accent "map" of the chorus:

x ! x x x ! x x ! x !
x ! x ! x ! x
! x ! x x ! x x !
x x ! x ! x ! x

If you count up the exclamation marks in each line, you'll find that the pattern for the number of accents in each line is 4 - 3 - 4 - 3, which answers the first part of your question.

Now to answer whether it's anapestic or iambic (or something else altogether), I looked at the second line and noticed that it is almost perfectly iambic (unstressed, stressed), except for the extraneous unaccented syllable. On the other hand, the very next line is missing an unaccented syllable at the beginning, which makes up for it. So my money is on this being iambic heptameter (because a line of four and a line of three add up to a total of seven iambs). To convince myself that I'm right about this, I go back and listen again, and everywhere I hear the singer doing "syllable cramming", I replace the crammed syllables with a single unaccented mark:

x ! x ! x ! x !
x ! x ! x ! x
! x ! x ! x !
x ! x ! x ! x

Aside from the fact that we have two lines that end with an extra unaccented syllable, this is iambic.

So now that you know this is a very "loose" iambic heptameter, you can go back to your version of the ballad, feeling confident of what the meter is. Your only challenges, then, are determining which syllables get stressed, and figuring out where the "syllable cramming" happens. Good luck!

Incidentally, as a side note, I think that the addition of those unaccented syllables at the end of each pair of lines gives it a sense of being unfinished, which adds to the melancholy feel of the piece.

After a few back-and-forth messages with Rosanna, here are a few more helpful tips for people trying to parse accented/unaccented syllables in a poem:

• Once you think you've figured it out, read it out loud, strongly emphasising (speaking loudly) the syllables you marked as stressed. This may help you identify mistakes you've made.
• If you know how many stressed syllables there are supposed to be in each line, that's very helpful information, because while a poet may mess with the unstressed syllables, they're less likely to change up the number of stressed syllables. 
• You're unlikely to find two stressed syllables in a row.

Judah asks a fairly lengthy question about musical instruments. In a nutshell, he's trying to understand the mathematics behind why musical instruments are not "perfect." His example uses stringed instruments like guitars and ukeleles. He comments that even on the best guitars, if the strings are perfectly in tune, pressing down the finger for a note higher up will never be "perfectly" in tune. He wonders why musical instruments can't be made "perfect." 

For starters, Judah, we should begin by noting that there really is no such thing as "perfect" - when the luthier puts the fret in place on the neck, how close to exact does he have to be for you to call it "perfect?" To the nearest 0.1 cm? To the nearest 0.01 cm? To the nearest 0.00001 cm? To the nearest molecular width? We should probably make our own definition of "perfect" - for our purposes we'll say a musical instrument is "perfect" if the difference between the actual note and the "perfect" note is not distinguishable to our ears. Perfection, then, will vary from one person to another. For example, I have a much better sense of pitch than most of my music students; they can play notes that they think are in tune, but I can tell that they're not. As you increase in musical ability, "perfect" (by our definition) becomes a bit of a sliding scale.

For our discussion here, let's say that being off by less than 0.1% is "perfect". This would mean that if you hear a note that is 439.5 hz, you can tell that it's not 440 hz.

You mentioned ukeleles and guitars, saying that ukeleles are more likely to have intonation problems, and here's the math behind that: the frequency of the note played is inversely proportional to the length of the string (the longer the string, the lower the frequency of the note). On a ukelele, that length is 33 cm, and on a guitar it's 63 cm. Let's say that a luthier can place a fret to within 0.05 cm of the proper position. On a guitar, that's 0.05 / 63 * 100 =  0.07% error based on the full length of the string. On the other hand, for a ukelele, that's 0.05 / 33 * 100 = 0.15%, which is roughly twice the percent error. This difference highlights the fact that it's possible for a luthier to make good guitars, but not be talented enough (or have good enough tools) to make ukeleles; he would need to have better tools, better precision, to make a satisfactory ukelele.

In theory, then, the larger the instrument, the easier it is to make it "perfect." But your question goes beyond what a luthier can do - you're saying that even if the luthier's work is "perfect', the guitar still isn't "perfect." Okay, so let's dive into some of the math more deeply. There's a formula (I had to look this one up - it's not one I remember off the top of my head!) for the frequency of a string:

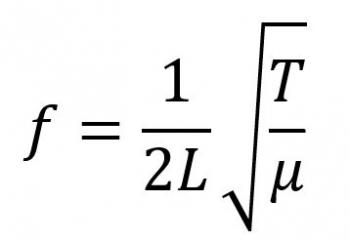
The important things for us to consider here are the L and the T. L is the length of the string (hence, the inverse proportion, because that is in the denominator) and T, which is the tension in the string. Note that the frequency is directly proportional to the square root of the tension.

You can easily see that this makes sense; when you tighten the pegs on your guitar, you are increasing the tension, and the frequency goes up. Similarly, when you put your finger down on the frets, you decrease the length, and in so doing, you increase the frequency.

So with this in mind, let's take a look at my guitar.

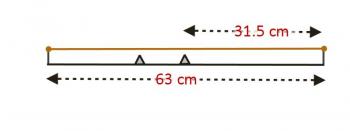
Here you can see the length from nut to bridge, with a couple frets shown, and the string above them. On my guitar, the length from nut to bridge is 63 cm. The vertical distance from the top of a fret to the string is 0.2 cm. Since the frequency is inversely proportional to the length, it stands to reason that if we have a fret halfway between nut and bridge, that'll be an octave (twice the frequency). So I've shown that fret. But wait...what happens when you press down? You now have this situation:

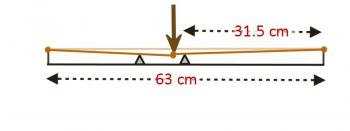
You've put your finger down behind the octave fret and pressed. In so doing, you did two things. First, you increased the tension in the string (thereby making the note sharper), but at the same time, you've also increased the length of the string being plucked (to see why, consider the right triangle shown below.

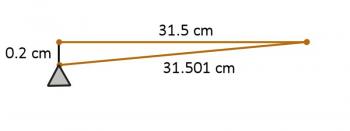
You've increased the tension (raising the note) and increased the length (lowering the note). Thankfully, these two changes are in opposite directions, so they help to cancel each other, rather than adding together. However, this means that a perfectly centered fret may not produce the note you want. Luthiers may use this information to compensate - on my guitar, the octave fret appears to be a very small fraction of a centimeter off-center. So even this issue can be resolved. Except...what if your finger is pressed closer to the fret behind the octave fret? Doesn't that change the tension, without changing the length?

But none of that is the big issue. That was just to get you thinking about the geometry of tension and length. The big issue is that we tend to think of musical instruments as static objects, when in fact they are not. Guitars, ukeleles, violins, cellos, etc are made of wood, and wood is a non-uniform, unpredictable substance. The moment the guitar leaves the luthier, it begins a lifetime of heat and cold, humidity and dryness, high pressure and low pressure, and all of these things affect the shape of the guitar. Anything that affects the shape will affect the intonation.

If the luthier doesn't pick excellent wood, it is prone to warping.  This tendency to warp is why (in construction) it is better to screw two 2x4s together instead of using a single 4x4; the two 2x4s are not likely to warp in the same direction, which means each 2x4 helps to prevent the other from warping, and you're more likely to get an unwarped structure.

Even if the very best quality of wood is chosen, humidity changes the shape of the guitar. This is why your guitar has a rod going down the neck, and an allen nut that lets you adjust the angle of the neck. Look at it this way: in the winter time (low humidity) you may be more likely to get fret buzz, because the strings are closer to the neck, and in the summer (high humidity) you might need to press harder on the strings, because the strings are further from the neck. Let's take that last idea, and really exaggerate it in a diagram:

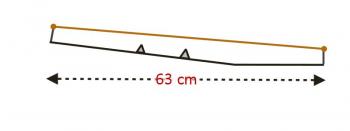
What does this do? The big thing is that it makes you press harder to get the string down, which significantly increases the tension in the string. BUT, the closer to the nut you get, the closer to the frets the string is, which means there's less pressure required, and the strings are less out of tune. So if you play an instrument and realize that the further up the fretboard you go, the more out of tune the guitar is, odds are good that neck needs to be adjusted.

There are undoubtedly many other things that come into play; I'm not an expert on the construction of musical instruments. But this will hopefully give you a good sense for some of the challenges in building - and maintaining - musical instruments.

One of the interesting things about all of this is that - as you mentioned - it's not necessarily a bad thing to have "imperfect" instruments. One of my favorite sounds in an orchestra is the violin section playing in unison way up high. It produces an ethereal sound, which can be directly attributed to the fact that none of the violinists are playing exactly the same frequency. That "cloud" of frequencies centered around the "right" frequency makes a wonderful sound. In fact, it's so wonderful that effect machines are designed to reproduce it - it's called a "chorus effect." A chorus effect creates multiple copies of the actual sound of a voice or instrument and shifts it slightly in time and in frequency to produce that almost-unison sound that is so wonderful to hear.

"I keep hearing about people who are good at math and music. But that seems so strange -- music is so artistic and flowery, while math is so technical and straightforward. How could either have anything in common with the other?" ~ Laura from Maine

Hi Laura, thanks for thre great question. I wish I could give you a solid scientific answer to this question, but the inner workings of the brain definitely are not in my field of study. Instead, I can give you some observations about both math and music, based on my own experiences as a mathematician and a musician.

First, I can confirm that what you said is typical in my experience - it is very common for people who are good at music to also be good at math (and vice-versa). Obviously, that's not a 100% rule (probably not even close!) but it is common enough that my high school math teacher used to refer to his best students as his "M & M students." Not because they liked chocolate in a candy shell, but because they excelled in both Math & Music.

So what's the connection? I'm going to suggest three connections: patterns, precision, and creativity.

Patterns in Music

Music is filled with patterns. That can be seen in the simplest of ways: a couple days ago I sat down with my five-year-old son and taught him a little bit about the piano. I showed him how to find the note C by looking for patterns. There are sets of three black keys, and there are sets of two black keys. C is any white key that comes right before a set of two black keys. From there, he could find any C on the keyboard. I showed him that the note names go from A to G, and then start over at A. From there, he could start at the low end of the keyboard and name every single white key on the piano. Patterns.

Eventually he will discover that there are certain intervals (major thirds, minor thirds, etc) that sound really nice together, and others that don't sound quite as nice. He'll discover that those intervals can be shifted up and down the keyboard by octaves, and then he'll discover that they can be shifted by other amounts, and the sound is just as nice. 

Musical compositions are also filled wtih patterns. Just listen to Vivaldi's Four Seasons, and you'll hear the same "figure" repeated throughout a movement. Starting on one note, and then on another note, then with some variations to the pattern, but always with a pattern that your ear catches and hangs on to. Some of the most memorable classical compositions are the ones that have memorable patterns that appear over and over (think of "dum-dum-dum-DUM" in Beethoven's fifth symphony, or the themes of Rossini's "The Barber of Seville" and "William Tell Overture" - and if you're not familiar with those two compositions, think of Bugs Bunny as a barber, or the Lone Ranger). 

Patterns crop up in more modern music as well - the pattern of verse-chorus-verse-chorus-bridge-chorus is one that gets repeated over and over again in popular music. Your brain processes those patterns even if you're not consciously aware of them.

As an added bonus: most of the patterns we notice in music have a mathematical reason why they exist. For example, an octave is an interval that sounds good because the frequencies of the notes are in a ratio of 1:2.

Patterns in Math

I'm not sure I even need to say that math is filled with patterns. It seems intuitively obvious. But let's consider just a couple things. First, I remember how fascinated I was when I first discovered the nine-times-table:

9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45...

...and so on. As the tens place increases by one, the ones place decreases by one, and in each case, the sum of the digits is 9. What a fascinating pattern.

Fibonacci was famous for discovering patterns, and exploring how they related to the natural world around us - for more on Fibonacci, you might want to consider this book, reviewed here by Book Scrounger: Blockhead: The Life of Fibonacci.

A couple days ago my son went for his yearly checkup, and his doctor commented that math learning at his age is all about finding patterns.

People who like looking for patterns will naturally be drawn to either math or music, or both.

Precision in Music

If you've ever taken music lessons, you understand this one. I remember, as a violin student, being expected to be very precise about a lot of things: how I hold the bow, how I hold the violin, where I put my fingers, how I draw the bow across the strings. And then I'd do scales over and over again, with my teacher telling me, "That C-sharp isn't sharp enough." or "Your bow is way down on the fingerboard." Getting good at playing a musical instrument requires a fairly stubborn and determined mindset to get it right. For a violin student, "getting it right" is sometimes a matter of a miniscule fraction of an inch one way or the other. 

So when you said that "math is technical," my response to that is: so is music! Students who can't master the technical aspects will not excel.

Precision in Math

The same stubborn, determined mindset that makes someone decide they're going to practice a D-major scale until they get it right is necessary for a good math student as well. In elementary school it's memorizing those math facts. Then it turns into more and more complicated processes (arithmetic algorithms, arithmetic operations on fractions), and eventually the student is faced with complex algebraic and even calculus problems. And good math students practice these over and over again (it's why those cruel and nasty math teachers assign homework; doing 20 math problems is like practicing your D-major scale over and over and over again). You don't get that kind of precision any other way.

People who have the determination to keep practicing things are more likely to excel in math or music, or both.

Creativity in Music

Eventually, every violin student who sticks with it long enough gets to the point where their teacher says, "Okay, it's time to learn about vibrato." What is vibrato? Vibrato is, according to one dictionary: "a rapid, slight variation in pitch in singing or playing some musical instruments, producing a stronger or richer tone." In a sense, vibrato is a breaking of the rules, because you've been trying desperately to play in tune, and now your teacher is giving you permission to play out of tune. In fact, your teacher is demanding that you play out of tune. In my mind, it was at that moment that I moved from parroting to interpretation. You are no longer at the mercy of the musical composition; the notes on the page become a vehicle for your own personal expression. And vibrato is just one thing - whatever musical instrument you play, as you advance, you will discover more and more that there are ways to express yourself through creative use of the technical skills you've acquired. You've become creative.

And, do I need to mention? Writing musical compositions is a wonderful task in creativity!

Creativity in Math

Really? Math is "creative"? Sure it is! Math is problem solving! Math is curiosity, and exploring beyond what is known. When I graduated from high school, on Class Night, my math teacher presented me with a our school's highest math award, and at the same time presented me with a notebook which contained every math problem I'd solved during my independent study math course that year. What's the big deal about that (you might ask)? The big deal is that every one of the problems I worked on that year was a problem I made up myself, or decided to challenge myself with. Whether it was proving the quadratic formula, deriving a formula for the inverse of an N x N matrix, developing my own theorems, or just posing mathematical questions to myself and trying to solve them, I spent the entire year being creative. And that creativity is what makes a mathematician. Being a good mathematician doesn't mean being able to multiply 324 x 16.9; that's just the precision practice (like learning a musical scale); being a good mathematician means being able to take those skills you've practiced, and put them to use in new  ways to solve problems you haven't solved yet.

When I have students who want to take my math classes as "honors level" classes, I expect problem solving from them; I expect them to take the things they've learned and put them to use in brand new ways that they've never thought of before. I expect them to combine two mathematical ideas that they've never used together before, and use them to develop a solution to a problem they didn't think they could solve. I expect them to get creative.

People who are willing to use the tedium of repeated practice to explore new ideas and new ways of doing things will excel at either math, or music, or both.

"There is geometry in the humming of the strings, there is music in the spacing of the spheres." ~ Pythagoras

An anonymous reader asks, "How do you get good at 'listening' for iambic pentameters?"

Poetry, like music, has rhythm. In music, the rhythm is established using a few different intstruments. In a band, the drummer and the bass guitarist are the primary rhythm-holders. Those deep, bassy sounds like the guitar and the kick (bass) drum set our subwoofers to vibrating, and mimic our own heart rhythms.  In some music, the rhythm is prominently defined by the kick drum and the snare drum. A GEICO ad from awhile back made this point with a pig singing "Boots and pants and boots and pants and..."

The words "boots" and "pants" represent the kick drum*, and the word "and" represents the snare. The kick drum provides the primary driving beat, and the snare represents what we call the "off-beat".

So the pig is actually giving you the beat of a song.

You can feel the rhythm of that if you repeat it over and over, and if you do it just right, it's almost indistinguishable from a techno band.

The rhythm of a poem (in poetry, we call it the "meter" of the poem) can be understood in terms of kick drums and snares, which means it can also be understood in terms of phrases like "boots-and-pants-and". In poetry, we have stressed syllables and unstressed syllables. Stressed syllables correspond to the driving "kick" beat, and the unstressed syllables correspond to the off-beat of the snare. So what does iambic pentameter look like?

and-BOOTS-and-PANTS-and-BOOTS-and-PANTS-and-BOOTS.

Notice that we start with the snare, or the off-beat, and we end with the kick. Also notice that we have 5 kick beats. This is why it's called penta-meter; "penta" is five and "meter" is rhythm, so pentameter is a five-rhythm.

The nice thing about having five kicks in a line is that you've got five fingers on one hand, so while you are saying "and boots and pants..." each time you say either "boots" or "pants" you can tap a finger on the table, and when you've tapped all five fingers, you've completed a line of the rhythm. So if you want to get good at listening for iambic pentameter, do this repeatedly. Say the "and-boots" pattern while tapping out the kick beat on your fingers. If you want, after you do the fifth finger, give a little pause, and then start all over again:

and-BOOTS-and-PANTS-and-BOOTS-and-PANTS-and-BOOTS [pause] and-BOOTS-and-PANTS-and-BOOTS-and-PANTS-and-BOOTS [pause] etc.

After awhile, that rhythm will get ingrained in you, and you'll be doing it without even thinking about it. Now let's take a look at something that's written in iambic pentameter:

The quality of mercy is not strain'd,
It droppeth as the gentle rain from heav'n
Upon the place beneath: it is twice blest;
It blesseth him that gives and him that takes. (Shakespeare, The Merchant of Venice)

If you've got that "boots-and-pants" thing going through your mind, it'll be easier to see that this is iambic pentameter:

the QUAL i TY of MER cy IS not STRAIN'D
it DROPP eth AS the GEN tle RAIN from HEAV'N
u PON the PLACE be NEATH: it IS twice BLEST;
it BLESS eth HIM that GIVES and HIM that TAKES.

Can you feel the rhythm of it?

Important Disclaimers

1. Thinking "and-boots-and-pants" may be a great way to recognize and understand the rhythm of poetry, but it is NOT a good way to read poetry; nobody wants to hear Shakespeare sounding like techno music**. Instead, you should use boots-and-pants to help you recognize where the beats are, but then once you've understood which syllables get the stress, you're going to read this in your normal reading voice, without giving unnecessary extra accent to any syllables.
2. Also, even though when you practiced the rhythm, you left a pause between lines, you won't necessarily do that when reading a poem. Focus on the meaning of the lines; if a line does not complete a thought, you're not going to pause at the end of it. And if a thought is completed within a line, you're going to pause there. Remember that meaning is most important, and rhythm serves the poem, not the other way around! So with this in mind, the Shakespeare piece would be read like this:

The quality of mercy is not strain'd, [pause]
It droppeth as the gentle rain from heav'n upon the place beneath; [pause]
It is twice blest; [pause]
It blesseth him that gives and him that takes.

Other Meters

The "boots-and-pants" idea can be used to recognize other meters as well. For example, if you want to get the feel for anapestic tetrameter, you should start thinking:

and-the-BOOTS-and-the-PANTS-and-the-BOOTS-and-the-PANTS.

Notice that we've added the word "the" after the word "and" each time. This gives the meter a "triplet" feel. Also note that we only hit four driving beats in a line instead of five. So if you're counting this on your fingers, leave out your thumb.

You can see this rhythm in the well known Christmas poem "Twas the Night Before Christmas":

twas the NIGHT be fore CHRIST mas and ALL through the HOUSE
not a CREA ture was STIRR ing not E ven a MOUSE

* Technically, "boo" and "pan" represent the kick, and the "ts" represents the hi-hat. Thus, we really break it down like this: BOO-ts-and-PAN-ts-and.

** Well, okay, maybe "techno-shakespeare" should be a thing. But I'm not sure your poetry teacher will appreciate it!