Judah asks a fairly lengthy question about musical instruments. In a nutshell, he's trying to understand the mathematics behind why musical instruments are not "perfect." His example uses stringed instruments like guitars and ukeleles. He comments that even on the best guitars, if the strings are perfectly in tune, pressing down the finger for a note higher up will never be "perfectly" in tune. He wonders why musical instruments can't be made "perfect." 

For starters, Judah, we should begin by noting that there really is no such thing as "perfect" - when the luthier puts the fret in place on the neck, how close to exact does he have to be for you to call it "perfect?" To the nearest 0.1 cm? To the nearest 0.01 cm? To the nearest 0.00001 cm? To the nearest molecular width? We should probably make our own definition of "perfect" - for our purposes we'll say a musical instrument is "perfect" if the difference between the actual note and the "perfect" note is not distinguishable to our ears. Perfection, then, will vary from one person to another. For example, I have a much better sense of pitch than most of my music students; they can play notes that they think are in tune, but I can tell that they're not. As you increase in musical ability, "perfect" (by our definition) becomes a bit of a sliding scale.

For our discussion here, let's say that being off by less than 0.1% is "perfect". This would mean that if you hear a note that is 439.5 hz, you can tell that it's not 440 hz.

You mentioned ukeleles and guitars, saying that ukeleles are more likely to have intonation problems, and here's the math behind that: the frequency of the note played is inversely proportional to the length of the string (the longer the string, the lower the frequency of the note). On a ukelele, that length is 33 cm, and on a guitar it's 63 cm. Let's say that a luthier can place a fret to within 0.05 cm of the proper position. On a guitar, that's 0.05 / 63 * 100 =  0.07% error based on the full length of the string. On the other hand, for a ukelele, that's 0.05 / 33 * 100 = 0.15%, which is roughly twice the percent error. This difference highlights the fact that it's possible for a luthier to make good guitars, but not be talented enough (or have good enough tools) to make ukeleles; he would need to have better tools, better precision, to make a satisfactory ukelele.

In theory, then, the larger the instrument, the easier it is to make it "perfect." But your question goes beyond what a luthier can do - you're saying that even if the luthier's work is "perfect', the guitar still isn't "perfect." Okay, so let's dive into some of the math more deeply. There's a formula (I had to look this one up - it's not one I remember off the top of my head!) for the frequency of a string:

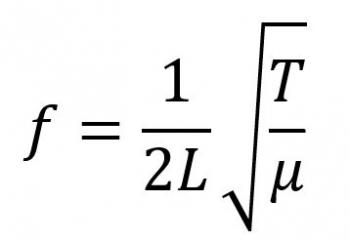
The important things for us to consider here are the L and the T. L is the length of the string (hence, the inverse proportion, because that is in the denominator) and T, which is the tension in the string. Note that the frequency is directly proportional to the square root of the tension.

You can easily see that this makes sense; when you tighten the pegs on your guitar, you are increasing the tension, and the frequency goes up. Similarly, when you put your finger down on the frets, you decrease the length, and in so doing, you increase the frequency.

So with this in mind, let's take a look at my guitar.

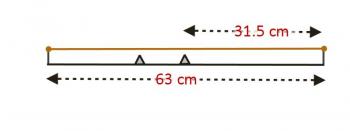
Here you can see the length from nut to bridge, with a couple frets shown, and the string above them. On my guitar, the length from nut to bridge is 63 cm. The vertical distance from the top of a fret to the string is 0.2 cm. Since the frequency is inversely proportional to the length, it stands to reason that if we have a fret halfway between nut and bridge, that'll be an octave (twice the frequency). So I've shown that fret. But wait...what happens when you press down? You now have this situation:

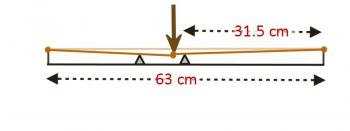
You've put your finger down behind the octave fret and pressed. In so doing, you did two things. First, you increased the tension in the string (thereby making the note sharper), but at the same time, you've also increased the length of the string being plucked (to see why, consider the right triangle shown below.

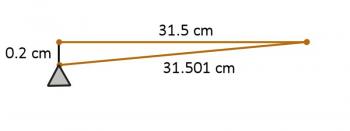
You've increased the tension (raising the note) and increased the length (lowering the note). Thankfully, these two changes are in opposite directions, so they help to cancel each other, rather than adding together. However, this means that a perfectly centered fret may not produce the note you want. Luthiers may use this information to compensate - on my guitar, the octave fret appears to be a very small fraction of a centimeter off-center. So even this issue can be resolved. Except...what if your finger is pressed closer to the fret behind the octave fret? Doesn't that change the tension, without changing the length?

But none of that is the big issue. That was just to get you thinking about the geometry of tension and length. The big issue is that we tend to think of musical instruments as static objects, when in fact they are not. Guitars, ukeleles, violins, cellos, etc are made of wood, and wood is a non-uniform, unpredictable substance. The moment the guitar leaves the luthier, it begins a lifetime of heat and cold, humidity and dryness, high pressure and low pressure, and all of these things affect the shape of the guitar. Anything that affects the shape will affect the intonation.

If the luthier doesn't pick excellent wood, it is prone to warping.  This tendency to warp is why (in construction) it is better to screw two 2x4s together instead of using a single 4x4; the two 2x4s are not likely to warp in the same direction, which means each 2x4 helps to prevent the other from warping, and you're more likely to get an unwarped structure.

Even if the very best quality of wood is chosen, humidity changes the shape of the guitar. This is why your guitar has a rod going down the neck, and an allen nut that lets you adjust the angle of the neck. Look at it this way: in the winter time (low humidity) you may be more likely to get fret buzz, because the strings are closer to the neck, and in the summer (high humidity) you might need to press harder on the strings, because the strings are further from the neck. Let's take that last idea, and really exaggerate it in a diagram:

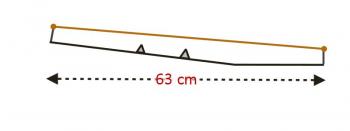
What does this do? The big thing is that it makes you press harder to get the string down, which significantly increases the tension in the string. BUT, the closer to the nut you get, the closer to the frets the string is, which means there's less pressure required, and the strings are less out of tune. So if you play an instrument and realize that the further up the fretboard you go, the more out of tune the guitar is, odds are good that neck needs to be adjusted.

There are undoubtedly many other things that come into play; I'm not an expert on the construction of musical instruments. But this will hopefully give you a good sense for some of the challenges in building - and maintaining - musical instruments.

One of the interesting things about all of this is that - as you mentioned - it's not necessarily a bad thing to have "imperfect" instruments. One of my favorite sounds in an orchestra is the violin section playing in unison way up high. It produces an ethereal sound, which can be directly attributed to the fact that none of the violinists are playing exactly the same frequency. That "cloud" of frequencies centered around the "right" frequency makes a wonderful sound. In fact, it's so wonderful that effect machines are designed to reproduce it - it's called a "chorus effect." A chorus effect creates multiple copies of the actual sound of a voice or instrument and shifts it slightly in time and in frequency to produce that almost-unison sound that is so wonderful to hear.