Jim writes: "I have included "My Secret Word" as a daily game for those in my private Facebook Group We play the game and post our scores and the last player each day posts the word when he or she solves he puzzle. Lately, when I follow the posted link address I do not get the same game as the others. Why is that? How can I fix that? Please help."

Jim, I actually sent you a reply email, but it got returned with a "mailbox unavaiable" message, so I'm posting my reply here, in hopes that you'll see it!

Wanshika from SriLanka asks, how to "identify stressed and unstressed vowels without pronouncing them loudly?"

That's a good question, Wanshika, and both Mr. and Mrs. Puzzler have an answer for you.

Mrs. Puzzler says, "Tap your hand on a desk for each stressed syllable." (Or, if you're trying to be extra quiet, tap on your leg!). What you'll find is that it's almost impossible to tap on the unstressed syllables; your brain somehow pushes you into doing the tap whenever your vocal chords are forming a strong syllable.

Mr. Puzzler says, "Tap on your leg with your thumb and your forefinger. If you're like me, you'll find that you gravitate toward tapping with your thumb on the stressed syllables, and the unstressed syllables with your forefinger." Mr. Puzzler's suggestion is really better for checking rhythms of poetry, if you already know where the accents are supposed to be.

If you try to tap this sentence out on thumb and index finger, then you'll find it has a perfect meter from the start to ending syllable.

[Note: the sentence above is written so that the first syllable is accented, and then it alternates between stressed and unstressed].

Related post: How context affects the way we stress syllables.

Mathi, from Vellore, wants to know how to figure out the following game show probability:

"On a game show, a contestant is given three keys, each of which opens exactly one of three identical boxes. The first box contains $1, the second $100, and the third $1,000. The boxes are randomly lined up and the contestant gets to assign each key to one of the boxes. The contestant wins the amount of money contained in each box that is opened by the key he assigns to it. What is the probability that a contestant will win more than $1,000?"

I'm not going to answer that exact question, because I think we can make it more challenging and interesting by changing the numbers a bit. Let's do this one instead:

"On a game show, a contestant is given four keys, each of which opens exactly one of four identical boxes. The first box contains $250, the second $500, the third $750, and the fourth $1,000. The boxes are randomly lined up and the contestant gets to assign each key to one of the boxes. The contestant wins the amount of money contained in each box that is opened by the key he assigns to it. What is the probability that a contestant will win more than $1,000?"

First, we need to figure out how many ways the keys can be arranged. The first key can be assigned in 4 ways, the second one in 3 ways (since one key has already been placed), the third key in 2 ways, and then there's only one way to place the last key. That gives us a total of 4 x 3 x 2 x 1 = 24 ways. So if we can figure out how many possibilities are wins, all we need to do is divide that by 24 to get the answer.

It's a win if you place all the keys in the right position. There is one way to do that.

It's a win if you place $1000 and any one of the others correctly. (Note that you can't place $1000 and two others correctly, because if you place three of them correctly, the fourth one must be correct as well, and we've already counted that possibility!). So there are three ways to do that.

It's a win if you place the $500 and $750 correctly (but not the other two, since we've already counted that possibility!). You can do that in one way.

And there are no other combinations that work. Thus, we have a probability of (1 + 3 + 1)/24 = 5/24.

Now that we've gone through that, you'll be surprised at how easy the other problem is - there are far fewer combinations to consider!

Good luck!
Professor Puzzler

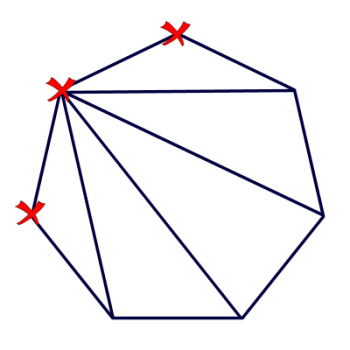
Ninth grader Michaela wants to know how you can "find the number of diagonals [in a polygon] drawn from a single vertex."

In answering this question, I'd like to point out that my diagram shows a convex polygon. If the polygon is concave, some of the diagonals will lie outside the polygon, but we would still call them diagonals.

If you look at the diagram to the right, you'll see that I've marked three vertices with an X.  Why? Because those are the vertices we can't draw a diagonal to.  You can't draw a diagonal from a vertex to itself, and you can't draw a diagonal from a vertex to its neighboring vertex. After all, drawing a line between two neighboring vertices isn't drawing a diagonal; it's drawing a side!

So, there are seven vertices in my polygon, and we can't draw diagonals to three of them, so that means we can draw diagonals to 7 - 3 = 4 vertices.

Can we generalize that? Of course! No matter how many sides the polygon has, there will always be 3 vertices you can't draw a diagonal to.

So if it has n vertices? You can draw n - 3 diagonals from any vertex.

As an added bonus (this goes beyond what you asked, Michaela!), this is how we get the formula for the number of diagonals in a polygon.

There are n vertices, and we can draw n - 3 diagonals from each one, making a total of n(n - 3) diagonals. Except...wait a minute! We've counted each diagonal TWICE (because we counted both endpoints!). So we need to divide that by two:

Total diagonals = n(n - 3)/2.

Enjoy your polygons!
Professor Puzzler

Karylle from Marinduque wants to know how you can find the ratio in an infinite geometric series, if you know that the sum is a particular multiple of the first term.

This is in that interesting class of problems in which you feel like you don't have enough information to solve it. After all, there are a lot of unknowns (the first term, the ratio, and the sum) and you'll only have one equation to work with. Whenever my students have problems like this, I tell them to simplify the equation as much as possible, and see what happens!

So let's take an example.  Let's say that you know the sum of the infinite series is 5 times the first term. Can you find the common ratio?

Well, the sum of the series is a/(1 - r), and that is 5a.

a/(1 - r) - 5a = 0

Ah...I see what's going to happen already - the a is going to factor out:

a(1/(1 - r) - 5) = 0

so either a = 0 (in which case, r could be anything, right? It's a really boring series, with all the terms equal to zero, but hey, it works!) or 1/(1 - r) = 5. This leads to:

5 - 5r = 1

5r = 4

r = 4/5

I would be inclined to say that the problem should be reworded to state that the first term is not 0, in order to avoid having "r can be any real number" as the answer. If you add in that proviso, then the answer is r = 4/5.

Hope that helps, Karylle!

Professor Puzzler