Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
What is the solution to the following puzzle that's been going around facebook?
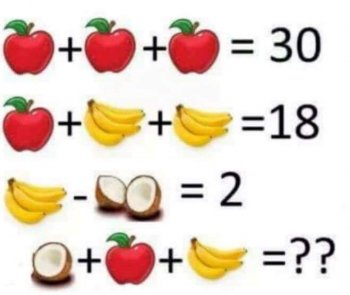
The answer is, on the surface, not terribly difficult to find:
3 apples = 30, so 1 apple = 10.
10 + 2 bananas = 18, so 2 bananas = 8 and 1 banana = 4
4 - 1 coconut = 2, so 1 coconut = 2
Therefore, 1 coconut + 1 apple + 1 banana = 2 + 10 + 4 = 16
HOWEVER...
Although this is the answer everyone seems to be giving, it's actually not correct. Notice that each bunch of bananas has four bananas (look closely!) except the one in the final line, which has 3 bananas. Also notice that the third line has one coconut, while the last line has only 1/2 of a coconut.
This changes things!
3 apples = 30, so 1 apple = 10.
10 + 8 bananas = 18, so 8 bananas = 8 and 1 banana = 1
4 - 1 coconut = 2, so 1 coconut = 2
Therefore, 1/2 coconut + 1 apple + 3 bananas = 1 + 10 + 3 = 14
This is a really nice problem, since it gives you a good reminder to pay attention to details!
Click the image below to read Professor Puzzler's analysis of another puzzle:

Addendums
William from Phoenix asks, "Apples coconuts bananas: The editing to remove the fourth banana was incomplete. it left the end point in the picture on line four. Was that intentional to cause controversy with your answers?"
Honestly, William, I can't see the incomplete erasure you're talking about. I don't doubt you, but I'm not seeing it. But, since you asked, I'll take this opportunity to point out: I didn't create this problem; I just wrote up the solution for people who wanted to know. If I had to make a guess, I would say that the person who created it did not intentionally leave part of a banana; they probably were just inexperienced with photoshop, or were in a hurry when they created it!
Colton from Florida had a question about the Algebra of this problem, which we answered here: Can X and Y have the same value?
Pany from UK points out that there is another way to interpret the problem, in which we regard each image as a symbolic variable, rather than as collections of real world objects. While I don't agree with him that this is the best way of looking at it, it is absolutely a valid way of viewing the problem, and it results in a very different problem, which is unsolvable, because we have more variables than equations. And speaking of which...
Anne from Maine shared with us a similar looking problem with a very different solution. Click the image below to read that post:



