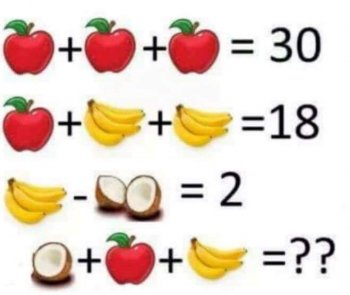Good morning, and happy 3rd day of Christmas. I don't have any French hens for you, but I do have a bit of a Christmas puzzle for you to work out. The first person to submit a 100% correct solution will win a Pro Membership on the site, which gives you access to many features that aren't publicly available (like creating your own mazes, interactive word games, and more).

So here's the puzzle. Every year we fill stockings on Christmas Eve. This year I had a problem - one of the items for my wife's stocking was too big to fit in the stocking. So I wrote instructions for where she was supposed to find the gift. But I didn't put the instructions in her stocking. Oh no, that would be far too easy. I cut the instructions up into six pieces (being careful to cut them in such a way that it would be difficult to interpret the instructions if even one piece was missing) and hid them in various places around the house.

Then I created five rebus puzzles, which - when solved - gave the clues to where the puzzle pieces were located. The rebus puzzles were then taped to various items in her stocking, so she would discover them one at a time as she unloaded her loot.

The rebus puzzles are below. Before trying to solve them, you should know that they are all references to items that are in our home. One of them is an item that is only in our home around Christmas time. Most of them are items that are in everyone's homes.  One item, I will tell you, is a map hanging on our wall. So to solve that rebus, you have to be able to tell me the location shown in the map. Another puzzle might require a google search.

Click on any picture to get a bigger version. When you think you know all six objects, click the "Ask your question" link at the top of bottom of the page to submit your answer. Once someone has solved all the puzzles, I'll post a note to that effect in this blog post. Sometime in January I will post the solutions to the rebus puzzles. Merry Christmas!

And by the way, if you enjoy rebus puzzles, there are books available on Amazon that have hundreds of these puzzles! Here's one that has over a thousand rebus puzzles:

Steve from Cincinnati writes: "I believe this puzzle answer is 1089.

11 X 11 = 4
22 X 22 = 16
33 X 33 = ???

"The first two equations are wrong, but they trick us into looking for a pattern rather than apply the mathematical rules...many people assume an addition function exists between each of the two pairs of integers. Not so. Therefore, thirty three multiplied by thirty three is 1089."

Hi Steve! Of course, you are 100% correct. 33 x 33 = 1089, no matter how many incorrect equations you put before it. Now that I've said that, if I stop there, I've got a really short blog post, and no one wants that - so let's fix their notation in order to turn it into a more interesting puzzle. We'll treat it as a single variable function:

Find x if:

F(11) = 4
F(22) = 16
F(33) = x

It still isn't a very good puzzle, though, because there's not enough information to come up with a single solution. In that respect, it's very similar to the "Squares Problem" I wrote up last year. Here are just three possible answers to the puzzle.

Solution #1
We add the digits of the number in the function's domain, and then square it. (1 + 1)² = 4; (2 + 2)² = 16; (3 + 3)² = 36.

Solution #2
We square the number, and then add the digits: 11² = 121 and 1 + 2 + 1 = 4; 22² = 484 and 4 + 8 + 4 = 16; 33² = 1089 and 1 + 0 + 8 + 9 = 18.

Solution #3
We subtract 8 from the number, and then add the quotient the number and eleven: 11 - 8 + 11/11 = 4; 22 - 8 + 22/11 = 16; 33 - 8 + 33/11 = 28.

I'm sure there are other solutions; those are just the ones that popped into my head on a quick glance. Can you come up with others? Send them my way and I'll add them to this post.

Veronica from Georgia asks, "A guy wants to buy a car and borrow $50,000. He gets $25,000 from his mom and $25,000 from his sister. He buys the car for $45,000. Driving home he runs into a friend that ask to borrow $3,000. You are now left with $2,000. You pay your mom and sister back $1,000 each and now you owe them only $24,000 each. After you pay them the $48,000 total to both, your friend pays you the $3000 he owes you. Do you know why the total comes out to $51,000 instead of $50,000 that you originally started out with?"

Hi Vernoica, This problem is very similar to the bellboy "missing dollar" problem, which you can read about by clicking the image below:

I'm going to use a slightly different approach in explaining this problem, by focusing on the meaning of positives and negatives in the context of transactions. Every financial transaction has a "direction." It is from one person (or organization/business, etc) and to another.  We use positives and negatives to indicate the direction of a transaction. We should choose a single individual as the focus for our problem, and once we've done that, every transaction will be signed based on whether the transaction is TO or FROM that person. In this case, the choice is obvious: the guy buying the car is the focus.

So let's agree that if a monetary transaction has "the guy" as the recipient, we'll call that transaction positive. If "the guy" is the giver, we'll call it a negative transaction. So we can list every transaction as a signed number:

Recieves $25,000 from his mother: +$25,000
Receives $25,000 from his sister: +$25,000
Buys car for $45,000: -$45,000
Lends $3000: -$3,000
Pay mother $1,000: -$1,000
Pay sister: $1,000: -$1,000
Pay mother $24,000: -$24,000
Pay sister: $24,000: -$24,000
Friend pays back loan of $3,000: +$3,000

So now that we have all of these transactions signed, we can add them up properly:

$25,000 + $25,000 - $45,000 - $3,000 - $1,000 - $1,000 - $24,000 - $24,000 + $3,000 = -$45,000

What does that -$45,000 represent? It represents the amount by which "the guy" has decreased his bank balance (the price of the car).

What does the number $51,000 represent? Absolutely nothing. Whoever gave you the problem picked three transactions out of the list of nine transactions, gave one of them the incorrect sign, and then combined them in a way that makes absolutely no sense in the context of the problem. Why would that add up to anything interesting? You got fooled into thinking it should mean something because it was so close to $50,000, which was a number that was mentioned in the problem. But adding those three quantities means absolutely nothing. When you give the numbers the correct signs, all the transactions cancel out to a single transaction - the cost of the car.

I'm Glad I've Got a Proofreader

In addition to occasionally writing math problems for this website, I've also written math problems for several states' math competitions. When I sit down to write problems, it's usually because I have to crank out a set of 100 math problems for a competition somewhere. When I'm finished writing them, I send them off to my proofreader. When he's proofreading, what do you suppose he's most likely to find?

1. spelling mistakes
2. grammar mistakes
3. arithmetic errors
4. algebraic errors
5. ambiguity errors

He does occasionally find spelling/grammar mistakes, but those are fairly infrequent. And yes, I do occasionally have arithmetic/algebraic errors! (When I'm writing a problem, sometimes I have to try two of three different things to make the problem work out correctly, and then I forget which things I've changed, and use numbers from the first version of the problem, and then my proofreader says, "Where in the world does this number come from?")

But the most common issue he finds is an ambiguity issue. Ambiguity simply means that students could reasonably interpret the problem in more than one way. If the student could interpret the problem in multiple ways, then it's a bad problem!

Here's a simple example:

In a right triangle, the sides are 5, x, and x + 1. Find the length of the hypotenuse.

Why is this ambiguous? Because I've implied that there's one answer ("find the length" instead of "find all possible lengths") but there are two possible answers, because the hypotenuse could be 5 (if x and x + 1 are less than 5) or it could be x + 1 (if x + 1 is greater than 5).

Here's another example:

Find the next term in this sequence: 5, 10, 15, ...

The obvious answer is 20, but that's not the only possibility; someone who is familiar with Fibonacci sequences could argue that this is the beginning of a Fib, and therefore the next term is 10 + 15 = 25.

These are just simple examples. The more complicated a problem is, the more likely it is to introduce something ambiguous without meaning to. So I'm glad I've got a problem proofreader.

The Internet Has No Proofreader

Now I put on my other hat - the "Professor Puzzler" hat. On any given day, this blog is a pretty quiet corner of the internet. This blog usually gets just a few hundred visitors per day. (Except on days we publish a new post, then the visitor rate climbs a bit).

But every once in awhile, something goes crazy. Back in February, for instance, there was one day where the traffic to the Professor Puzzler blog was 100 times it's normal rate. We had over 25 thousand page views on just one page of the blog.

Whenever this happens, it's invariably because someone posted an ambiguous (bad) math problem on the internet, and someone linked to our explanation of why it can't be solved.

And I realized something, after the most recent one: the majority of math problems posted on social media are ambiguous. The internet has no proofreader.

If you're interested to see some of the ambiguous/bad problems we've talked about in this blog, here are links to some of them. Just click on the image to jump to the corresponding blog post.

The most recent one was "The Flower Problem" or (as one site called it) "Pollen Pandemonium." This problem is straight-up ambiguous (and no, it was not part of a kindergarten exam in China; give the Chinese some credit, will you?). The most appropriate interpretation is to say that each distinct flower image represents a different variable. If that's the case, you have a system of three equations in four unknowns, which is unsolvable. If you operate from the assumption that the problem must have a solution, you reject the most appropriate interpretation, and then there is no way to solve it without making an assumption about what the writer intended. Each assumption will lead you to an answer, but depending on the assumption you make, you'll get a different answer. So the internet is full of people arguing for their interpretation, when the reality is, every solution is based on an unwarranted assumption.

The square problem is also ambiguous in the same way that my sequence problem above is ambiguous; there are multiple ways of interpreting the intent of the problem writer, and there isn't one right answer; there are many possible answers. But the problem is great for click-bait sites, because people will spend all day arguing their answer in the comments.

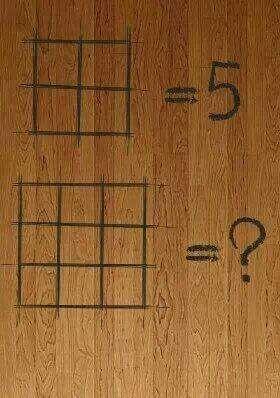
And there you have it: a history of bad math problems on the Ask Professor Puzzler blog. Click-bait sites love problems like this, because they generate arguments, and arguments turn into page views, comments, likes, and notoriety.

Math teachers, on the other hand, hate them...except as teaching tools about ambiguity!

Update June 20, 2016: One wise commenter responded to this blog post by saying "So people would rather argue, pretending unsolvable problems are solvable, than accept the simple fact that the problem was badly phrased to begin with. Seems this could have applications to Internet interactions far beyond the math realm!"

Can't argue with that!

DailyMail.co.uk, and the various click-bait sites that copy their content, seem to be a bit confused on the difference between "hard" and "unsolvable." They recently discovered the "flower problem" (which everyone else was talking about four months ago), then they found our explanation of the problem, and posted a fine click-bait article headlined something along the lines of "Problem is so hard even a math teacher can't solve it."

There is a huge difference between something being "hard" and something being "unsolvable."

Let me give you an example:

John can mow lawns at a rate of 1 lawn every three hours. Jane can mow lawns at a rate of 2 lawns every five hours. If John and Jane work together, how many brick walls can they build in ten hours?

This is not a hard problem. It's actually very, very easy. It's very easy to recognize that the answer is "not enough information given." Information about rates mowing lawns doesn't tell us a blessed thing about their wall-building rates.

"Hard" implies that someone will actually spend a lot of time wrestling with the problem. But, in fact, you didn't spend any time at all on that, right? You knew immediately and instinctively that there wasn't enough information to solve it. That wasn't hard.

Here's another problem:

If x + y = 30, find the value of 2x - 3y.

Now this one is a little harder, because it might not be immediately apparent that there isn't enough information to solve the problem. Any first or second year Algebra student, however, shouldn't spend much time on that before they say, "Hey, wait a minute! There are two variables there, and only one linear equation, so I can't find x and y!"

Of course, a problem can be both hard and unsolvable. I used to get (on a regular basis) emails from people all over the world who were convinced that they had found a method of trisecting angles with a compass and straight edge. They spent hours and hours on their solutions - it was hard. And, sadly, despite all their hard work, they were wrong; the correct answer is, "It can't be done." And it has been proven. And the proof wasn't an easy one.

But...the flower problem is not hard.* It's very easy to see why the problem is not possible to solve. If you think you've found a numerical solution, make sure you think through exactly what assumptions you've made about the flowers and their petals (and their stems and leaves, because yes, you've probably made assumptions about those, too!), and then go read our blog post.

Thanks for visiting our site, and make sure you try out our educational games while you're here!

* Having said that the problem is not hard, I have to admit that it's excruciatingly painful to look at the comment sections on sites like DailyMail and realize that even setting aside the fact that you can't solve the problem without making assumptions, most people posting their "answers" don't even know elementary level mathematics and order of operations, and that there are almost as many answers given as there are comments made. So maybe the problem is harder than I thought. 

And maybe DailyMail should have titled their article "So hard people think it can be solved." :D

For those who are interested in seeing more "bad math problems" on our blog, click the image below.