I don't normally do follow-up posts on subjects I've already written up, because most of the time when I get e-mailed questions or comments about things I've written, I feel like they are best suited to a discussion in our community forum, rather than creating extra blog posts. However, this particular question, even though it is a follow-up to the Apples, Bananas, and Coconuts blog post, is worth analyzing in its own right, independent of the previous blog post.

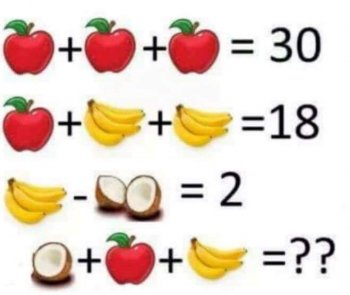
In the image shown here, the challenge was to find the value of an apple, three bananas, and half a coconut. There are multiple ways of assigning meaning to the images. For example, your basic banana "unit" could be 1 banana, or it could be 1 banana bunch (in which case, the last line contains 3/4 bunch!).

Similarly, your basic coconut unit could be a coconut, or a half-coconut. How you define these will affect how you work out the problem, but does not affect the solution.

One reader was concerned by the fact that you can end up with two variables having the same value: a half-coconut has the same value as a banana, and "this is not algebraically correct, as in algebra, X & Y cannot both be equal to one."

And this is the question we're exploring here: Can two variables have the same value in a problem?

The question-writer is not the only one who gets flustered by this possibility -- I have algebra students who get flummoxed every time I give them a problem in which both X and Y have the same value; they are convinced they must have done something wrong! In fact, just last week I gave my algebra students a system of three equations in three unknowns, in which the variables x, y, and z all were equal to one.

Really, there is no algebraic reason why two variables can't have the same value.

First, let me give you a graphical representation of an equation. Consider the following equation: y = 4 - x. If you graph it, it looks like this: 

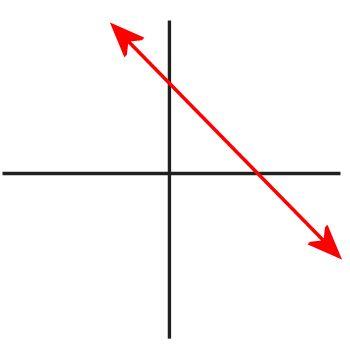
But what does that graph mean? It is simply a graphical representation of every ordered pair (x,y) that satisfies the equation. The red line is an infinite series of x and y values that make the equation true. But did you realize that there's a point in that graph for which x and y have the same value? It's true! It's the point x = 2, y = 2, because 2 = 4 - 2. If having two variables with the same value was illegal, then your algebra teacher would have taught you to graph the equation like this instead, leaving out the point (2,2):

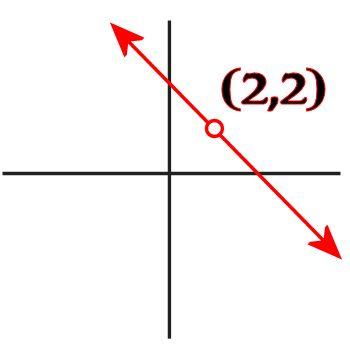
But your teacher didn't tell you to graph lines like this. Why? Because it's perfectly okay for two variables to have the same value!

There are practical implications that would result from supposing that x and y can't have the same value, because algebra was designed to have real-world application. Imagine an accident reconstruction expert is trying to figure out what happened when two vehicles collided. He sets up equations, assigning variables to all his unknowns, plugs in the values he does know, and then calculates the values of his uknowns.

Then, when he gets to the end of his calculations, he says, "Wait! This accident can't possibly have happened! Because the initial speed of the first car was 45 mph, and the initial speed of the second car was also 45 mph! We can't have the same value for two variables!"

No, of course he doesn't say that! In fact, if the speed limit was 45 mph, he'll just smile and say, "At least they were both going the speed limit!"

Or suppose you go shopping, and you pick up a bag of apples and a bag of pears. The bag of apples has 20 apples, and costs $4.00. The bag of pears has 10 pears, and costs $2.00. You think, "I wonder what is the cost of a single apple, and the cost of a single pear?" So you do set up two equations: 20a = 4 and 10p = 2, and to your horror, find that both apples and pears cost the same per fruit "That can't be right," you say, as you hurriedly put the fruit back on the shelf, "I had two variables, and they both came out to the same value!"

Of course not! You'll buy the apples and the oranges at the same unit price, and the universe won't explode! Because, you see, the real world doesn't really care about whether two quantities are equal or not. The values are what they are, and life goes on.

Someday I'm going to write a system of 26 equations in 26 unknowns, in which all 26 variables have the same value. My students' brains might explode, but nothing else will!