Fourth grader Alice asks, "How many diagonals are in decagon?"

Great question, Alice. But instead of giving you an answer to that question, I'm going to show you how you can figure it out for yourself. And not only that, I'll show you how you can figure out the answer for any polygon, even if it has 20, or 50, or 2000 sides!

Ready? Let's start with a simple example. We'll go with a polygon that has 8 sides (which is called an octagon), like this:

Now, this polygon, because it has eight sides, also has eight vertices. It seems a bit overwhelming to try to figure out all the diagonals, so let's just focus on one vertex. How many diagonals can you draw in an octagon, that all begin at one vertex?

The answer to that question is five. Take a look at the diagram below:

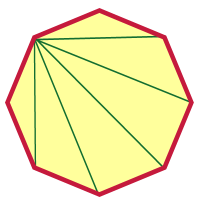
In this diagram I've chosen the diagonal to the left just below the top vertex, and I've drawn diagonals to every vertex that I can draw a diagonal to. Which diagonals can't I draw diagonals to? Well, I can't draw a diagonal from a vertex back to itself, and I can't draw diagonals to the two vertices next to that one (because those wouldn't be diagonals; they'd be sides!).

So there are three vertices I can't draw diagonals to from that vertex. Eight vertices total, minus the three I can't draw to, leaves five. That's important to remember: subtract 3 from the number of vertices, and you have the number of diagonals you can draw from any vertex.

But that's just one vertex! You could draw diagonals from any vertex, right? Sure! And there are eight vertices in our octagon, so we take the number of diagonals per vertex, and multiply it by the number of vertices: 5 x 8 = 40.

You might be tempted to think that that's our answer, but it's not. Why not? Because we've counted every diagonal twice! Every diagonal has two vertices, so we've counted it from one end, and we've also counted it from the other end. So to get the actual number of diagonals, we have to divide our answer by 2. 40 / 2 = 20. There are twenty diagonals in an octagon.

Let's try that reasoning on a polygon that has 2000 sides. Now, I'm not going to draw a 2000-gon for you; we'll just have to work out the reasoning without a picture.

1. Pick a vertex. How many diagonals can you draw from that vertex? Answer: 2000 - 3 = 1997.
2. How many vertices total? Answer: 2000
3. How many diagonals counted from all the vertices? Answer: 1997 x 2000 = 3,994,000
4. Oops! We've counted each diagonal twice! How do we get rid of the duplicates? Answer: 3994000 / 2 = 1,997,000

So a 2000-gon has 1,997,000 diagonals!

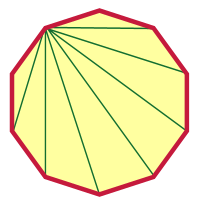
After doing something as crazy as a 2000-gon, a decagon shouldn't seem so difficult, right? I'll get you started, and you can finish it from here. I picked a vertex and drew diagonals from that vertex.

How many are there? Were you able to figure out how many there were without looking at the picture?

Can you figure it out from here? I hope so! Good luck, Alice. 

By the way, there is a formula you can use; it looks like this: D = n(n - 3)/2. But honestly, I don't expect my students to memorize it. I expect them to remember how we reason it out here. If you understand the logic, it's even better than having a formula!