Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Several months ago, Professor Puzzler wrote a blog post about the math problem "three over two x" (3/2x) and how it should be interpreted. The answer was: that's not a math problem; it's a typographical error, because fractions written with a diagonal bar, by typographical standards, should be written with the numerator a superscript, and the denominator a subscript, making it obvious whether the x is a part of the denominator, or separate from the fraction altogether.
A similar question has cropped up, and someone asked the Professor about how to interpret it: what is the answer when you perform the following operations:
6 ÷ 2(1 + 2)
This is another one of those facebook memes that people love to argue endlessly about. The primary arguments go as follows:
Argument #1
Do the parentheses first, giving you 6 ÷ 2 x 3. Now do the multiplication, giving: 6 ÷ 6. Now do the division and the answer is 1.
Argument #2
Do the parentheses first, giving you 6 ÷ 2 x 3. Now do the division, giving: 3 x 3. Now do the multiplication and the answer is 9.
Argument #3
Do the parentheses first, giving you 6 ÷ 2(3). Now do the parentheses (again), giving: 6 ÷ 6. Now do the division and the answer is 1.
Which of these arguments are valid?
Argument #1 is invalid, because once you're left with just division and multiplication, you do them from left to right. Multiplication does not take precedence over division! If you used argument #1, you should review BODMAS (PEMDAS).
Argument #2 is an acceptable argument. Here you're doing the multiplication and division from left to right, as required.
Argument #3 is also invalid, because "doing parentheses" means evaluating what's inside the parentheses, not combining them with things outside the parentheses.
Does that mean the answer is unequivocally 9? Or is there another argument to be made?
I'm going to stir the pot a little and suggest that there is another argument you could make.
Argument #4
BODMAS (PEMDAS) is a set of rules that is designed to tell us what to do with specific arithmetic operation graphemes*, and if we represent an arithmetic operation with a grapheme outside the set of graphemes, all bets are off.
* A grapheme is a visual, symbolic representation of something. For example, "A", "1", "÷" are all graphemes.
If you don't believe that using different graphemes can alter the order in which we do the problem, consider the following. Division can be represented by the symbol "÷" or by a vinculum (a horizontal fraction bar). With that in mind, are the following equivalent expressions?
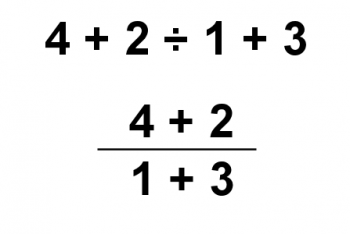
The answer is: of course they're not the same! The top expression is evaluated with 2 ÷ 1 calculated first, and then 4 + 2 + 3 = 9.
In the second expression, we evaluate the numerator and denominator first, giving 6 ÷ 4. Which gives 3/2 as the answer.
But they are both graphical representations of division! So why does the order of operations change? I tell my students that the vinculum is a "grouping symbol." In other words, it has implied parentheses. If you wanted to write it without the vinculum, you would have to add parentheses to the expression:
(4 + 2) ÷ (1 + 3)
Thus, even though the vinculum and "÷" are both division symbols, order of operations does not apply to them in exactly the same way.
In the same manner, one could argue that multiplication written with a different grapheme (in this case, the grapheme would be no grapheme at all) doesn't need to be interpreted in exactly the same way as multiplication written with the standard "x" grapheme. You could argue that in the same way that a vinculum as the division grapheme introduces implied parentheses into the problem, an empty grapheme for multiplication also introduces an implied grouping. In other words, 2(2 + 1) is actually an implied group: [2(2 + 1)]. This would change the answer to the original problem to 1 instead of 9.
And I would be hard pressed to provide a compelling argument against your interpretation, since I just got done telling you that a vinculum introduces an implied grouping!
Which leads us to the point I wanted to make from the beginning:
This is one of the reasons why, once we hit Algebra, we avoid using the ÷ grapheme for division. We almost entirely use a vinculum for division. Partly, that's because it allows us to be more compact in writing problems. But also because it becomes an implied grouping for division (allowing us to skip writing parentheses all over the place) AND it also avoids any chance of ambiguity that might arise from the question of how we write our multiplication. If a no-grapheme multiplication occurs under the vinculum, then it already has an implied grouping which it receives from the vinculum!


