Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Seventh grader Joe asks, "Can you come up with a better approximation to the Golden ratio than the fraction 8/5?"
Hi Joe! The answer to that question is: definitely!
Before we dive into approximations, do you know how to write the exact value of the golden ratio? It's (1 + √5)/2. If you punch that in your calculator (be sure to include the parentheses!) you'll get approximately 1.618.
The fraction 8/5 is 1.6, which is not bad, but we can definitely get closer!
One way to do it would be to take the golden ratio and shift the decimal one place, drop of everything after the decimal, and then put it over ten.
16/10
Of course, you can do the same thing, and get a better approximation, by shifting the decimal twice and dividing by 100:
161/100
Or 1618/1000. You get the idea, right? But that's kind of a cheater way of doing it, because it requires you to already know the value of the golden ratio!
So let's talk for a moment about how someone came up with the approximation 8/5. There's a very simple method for arriving at that fraction, and once you know the method, you can create your own approximations.
Are you familiar with the Fibonacci Sequence? It's a list of numbers. The first number in the list is 1, the second number in the list is 1, and each number after that is the sum of the two previous numbers in the list.
F1 = 1
F2 = 1
F3 = 1 + 1 = 2
F4 = 2 + 1 = 3
F5 = 3 + 2 = 5
F6 = 5 + 3 = 8
F7 = 8 + 5 = 13
F8 = 13 + 8 = 21
F9 = 21 + 13 = 34
Now if you look at those numbers, you might notice that F5 = 5 and F6 = 8. Those are the two numbers in your ratio! That might get you wondering...what if I picked two other adjacent Fibonacci numbers? Like 13 and 8? Well, 13/8 = 1.625, which is bigger than the golden ratio, but is closer to it than 1.6. So let's try the next two numbers in the sequence: 21/13 = 1.61538... This is smaller than the golden ratio, but is closer still! 34/21 = 1.619... Closer still!
You get the idea, right? If you take any two fibonacci numbers that are adjacent to each other, and divide the larger one by the smaller, you'll get an approximation of the golden ratio. The further down the list you go, the more accurate your approximation is.
For example, to pick two really big Fibonacci numbers: 317811/196418 = 1.618033988738303...
This is accurate to ten decimal places! Of course, it's not easy to remember, and it also isn't very easy to use. Whereas, 8/5 is both easy to remember and easy to use.
So 317811/196418 is better, but only in the sense that it is more accurate. It might be a good way of impressing your friends (or even your teacher), but that's about all it's good for.
Thanks for asking, Joe!
As an added note to this, below is an interesting graph which can help you visualize the approximations that you get by taking ratios of successive terms of the Fibonacci sequence.The horizontal orange line represents the golden ratio. The jagged blue line that alternately goes above and below the golden ratio is the sequence of ratios.
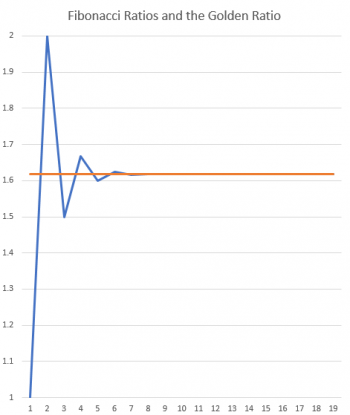
For example, the first point is 1/1 = 1, the second point is 2/1 = 2, and the third point is 3/2 = 1.5. After that, the sequence quickly converges on* the golden ratio, so that after the eighth or ninth value, you can't even see the blue line any more. That doesn't mean that those approximations equal the golden ratio; just that the difference is so small that it's less than a pixel on the screen!
No two of the ratios are the same value. They alternately flip back and forth between being too large and being too small forever, with the difference between the approximation and the actual value getting closer and closer to zero.
* "converge" is a mathematical term that means (roughly) "getting closer and closer to a certain value, without ever reaching it."

