Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
This week, hurricanes are on everyone's minds. In the aftermath of Hurricane Harvey, Hurricane Irma has become one of the most powerful hurricanes (currently at 185 mph sustained winds) in recorded history, and is bearing down on the Caribbean Islands, and is expected to make landfall in Florida.
I received a question from a Florida resident today. Kathryn would like to know how long she can expect to be in Hurricane Irma. Before I answer the question, I would like to make one thing very clear:
Disclaimer: this should not be taken as a scientific or meteorological prediction, and should under no circumstances be taken as any sort of recommended course of action. It is provided merely as a matter of curiosity.
Kathryn, instead of simply giving you a number, I'm going to develop a formula, to calculate the length of time. I realize you may not be interested in the mathematics behind the answer; if you aren't, you can simply skip to the bottom of the post where I use the formula to give you your answer.
The tricky part of answering this question is that the amount of time you are "in" the hurricane depends not just on the size and speed of the hurricane, but also how far from the center or eye of the storm you are. For example, if you pass directly through the center of the storm, you'll be under the storm for much longer than if the center of the storm passes 100 miles from your house. You'll still be under the storm, but not for as much time. So to answer the question, we'll need to know how far the eye is passing from your house. We'll call that distance D.
In developing the formula, we'll use several variables. Although we know how big Irma currently is, and how fast it is currently traveling, we don't know that those will be the conditions when the hurricane makes landfall. So instead of using 405 miles as the diameter, or 15 mi/hr as the speed, I'll use R for the radius of the hurricane, and V for the velocity. So when the hurricane approaches, if you can find updated data about the hurricane, you can plug those numbers into the formula.
Okay, now let's take a look at a picture.
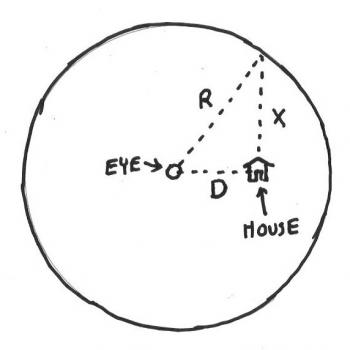
In the diagram, the large circle is the hurricane, the small circle in the middle is the center, or eye, of the storm. D is the closest distance the eye will pass to the house. The variable X will represent the distance the storm travels from the point where the eye is closest to the house until the house is no longer under the storm. That actually means that the house will be under the storm for a distance of 2X (since it travels X miles until it's closest to the house, and then another X miles before the house is out from under it).
The dotted triangle is a right triangle, which means we can use the Pythagorean Theorem to get X in terms of R and D:
X = SQR(R2 - D2) miles
Thus, the storm travels 2X = 2SQR(R2 - D2) miles. Since it is traveling at V miles per hour, the amount of time the house is under the storm is given by this formula:
T = 2SQR(R2 - D2)/V
Applying the Formula
In your case, you want to use the number R = 202.5 (you gave me a diameter of 405 miles, so I cut that in half to get the radius). The speed you gave me was 15 mi/hr, so V = 15. We don't know how close the eye is going to be to your house, so we'll do a worst-case scenario, and assume that the eye passes directly over. That means D = 0.
T = 2(SQR(202.52 - 02))/15 = 27 hours
As a reminder, that is based on data which is likely to change, and the assumption that the hurricane passes directly overhead. It's possible that, as the hurricane gets closer, you'll be able to find tracking information that helps you figure out how close the center of the hurricane will pass to you. If you find that information, you can plug it in to the formula in place of D (measured in miles).
For example, if you heard a news report that said, "Hurricane Irma will pass 100 miles west of city X" you would use 100 for D:
T = 2(SQR{202.52 - 1002))/15 = 23.5 hours
Finally, I'd like to reiterate that this is not provided as a scientific prediction or advice. The only advice I have to share with you is the advice my four-year-old son gave: "I hope Kathryn stays safe!" Please be careful and stay safe, Kathryn, and everyone else in the path of the hurricane!
Follow-up: Read Professor Puzzler's post-hurricane analysis of the formula's accuracy.
Professor Puzzler's PSA: Don't be taken in by Hurricane Conspiracies!
Added note: On my first day back to school with my high school math students, we explored the math question above, plus the following related (and slightly more challenging) problem: How long until the hurricane reaches me? This was a timely way of seeing a real-world application of geometry and trigonometry, as well as an opportunity to talk about hurricanes in general.

