What is the "altitude to the hypotenuse," and how do I find its length, if I know the lengths of two legs?

To answer this question, consider the diagram below. I show a triangle with angles A, B, and C, and right angle at C. The segment CD is the altitude to the hypotenuse. An altitude is a line segment that is perpendicular to a side, and passes through the opposite vertex. Thus, the altitude to the hypotenuse is perpendicular to the hypotenuse, and passes through the point C.

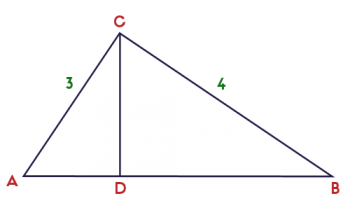
For this example, I gave the legs lengths 3 and 4. I did this so it would work out simply: the hypotenuse is 5 (because 3² + 4² = 5²).

The question is, how do we find the length of CD? To figure this out, it is helpful to notice that all three triangles are similar. 

ΔABC ~ ΔACD ~ ΔCBD 

From this, we know that the ratio of the longer leg to the hypotenuse is the same for each triangle.

In the largest triangle, that ratio is 4/5.  In the smallest triangle, that ratio is CD/3.

Thus, 4/5 = CD/3, which leads to CD = 12/5.