Chanchal from Muktsar asks if we could prove that in a quadrilateral the sum of exterior angles is 360°.

Good morning, Chanchal. One of the challenges of doing proofs on this blog is, a proof is constructed from the building blocks of things we already know, stacked together to create something we don't already know, and since I don't know you, I don't know what building blocks (knowledge) you have that you can build from. So before I start talking through the proof, here are some of the building blocks I'm going to use - in case you don't already know these things:

• the sum of the interior angles in a triangle is 180°
• when two lines intersect, they form four angles that add to 360°.
• vertical angles are congruent (vertical angles are the angles across from each other formed by two intersecting lines)

Okay, with that as background, let's look at a diagram.

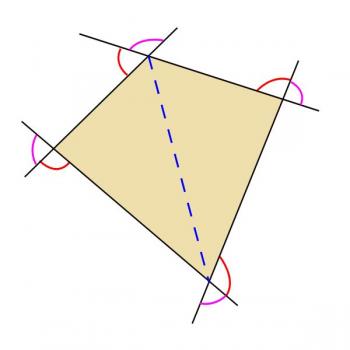
Now, my diagram is not just a quadrilateral - I've added some extra lines into it.

• The blue dashed line is a diagonal of the quadrilateral
• The sides of the quadrilateral have been extended to form exterior angles
• The purple arcs indicate angles which are opposite (vertical) to the interior angles of the quadrilateral
• The red arcs indicate the angles we're interested in.

Note that when we talk about the exterior angles of a quadrilateral, we're not talking about all the angles formed by the sides that lie outside the quadrilateral. We're not including the purple angles, and we're also not including the angles opposite the red ones. The exterior angles are all the angles "facing the same way" around the quadrilateral. That's not a very precise way of describing them, but hopefully you can see from my picture what I mean by that.

Okay, so how do we prove this? I'll give you two methods, and you can decide which one you like best. Ready?

Proof #1

• A quadrilateral can be divided into two triangles by a diagonal
• Each triangle has 180 degrees
• 180 x 2 = 360, so there are 360 degrees in the interior of a quadrilateral.
• Call these four angles a, b, c, and d. Then a + b + c + d = 360
• Each angle is supplementary to an exterior angle.
• Thus, the exterior angle measures are 180 - a, 180 - b, 180 - c, and 180 - d
• Adding these together gives (180 - a) + (180 - b) + (180 - c) + (180 - d) = 720 - (a + b + c + d)
• Since a + b + c + d = 360, this is equal to 720 - 360, which equals 360 degrees.

Proof #2

(Proof #2 starts out with some of the same steps as Proof #1)

• A quadrilateral can be divided into two triangles by a diagonal
• Each triangle has 180 degrees
• 180 x 2 = 360, so there are 360 degrees in the interior of a quadrilateral.
• Call these four angles a, b, c, and d. Then a + b + c + d = 360
• The intersecting lines at the four vertices form angles adding to 360 degrees
• Since there are four such sets of angles, their measures add to 360 x 4 = 1440 degrees.
• The purple angles from vertical pairs with the interior angles, so their measures are a, b, c, and d
• Thus, the sum of the red angles and their vertical counterparts is 1440 - (a + b + c + d) - (a + b + c + d) = 720 degrees
• Since vertical angles are congruent, we divide this sum in half to obtain the sum of the red angles: 720 / 2 = 360 degrees.

Incidentally, this proof can be extended to show that this is true not just for quadrilaterals, but for any polygon; the sum of the exterior angles is 360 degrees, regardless of the number of sides.  Thanks for asking, Chanchal!