Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Wesley asks, "I have been reading your answers to the corona virus questions and came across the term logistic curve. I am interested in the math behind them, and do not see how you can make a logistic curve unless one of two things. One, you take the inverse of an odd degree polynomial or two somehow you can incorporate the last y-value to influence the next x-value. I have come across this problem before and I would like to know if there is an alternate solution that can make a logistic curve an actual function of y in terms of x. If there isn't, thank you anyways for your time and effort."
That's a great question, Wesley. I like your thinking regarding odd degree polynomials. Odd degree polynomials do have an inflection point similar to a logistic curve. The problem with polynomial equations is that they don't have asymptotes. An asymptote is a straight line that the graph approaches without ever touching. A simple example of a graph with asymptotes is xy = 1. That graph gets closer and closer to the x and y axes, but never touches it.
A logistic curve has two horizontal asymptotes - one at the base of the curve, and one at the top. So a polynomial function (even an odd one) won't do the trick. What we need is an exponential function. Here's what you're looking for:
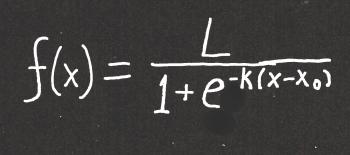
A "normal" exponential function might look something like this: f(x) = ekx. k controls how quickly the function "blows up" and x is the independent variable. Since we're thinking about virus spread, the independent variable is time - perhaps the number of days that have passed.
The logistic curve has elements of an exponential curve. It's interesting that the "e" is in the denominator, and also that it has a negative exponent - those two features sort of "cancel" each other out, because a negative exponent indicates taking the reciprocal. But it's the other stuff in the denominator with the e that makes this function's behavior interesting.
First, if x < x0, then the exponent of e is a positive number, and the denominator will be growing larger the further x is from x0. This results in a large denominator, which results in the value of the fraction approaching 0.
On the other hand, if x > x0, then e has a negative exponent, which means it is getting closer and closer to 0. This means the denominator is getting closer and closer to 1, and the function value is getting closer and closer to L.
This gives us our two asymptotes: y = 0 and y = L. Thus, 0 < f(x) < L.
And the point x = x0 is the point at which the function switches from blowing up to leveling off.
TO SUMMARIZE: in the logistic curve, k determines the rate at which the function grows, L represents the maximum value, and x0 represents the point in time at which the graph has its inflection point. In terms of a viral infection, L is the number of people who will be infected, and x0 is the time at which the number of new infections begins decreasing.
Wesley writes, "Is there a better way of factoring polynomials other than guess and check? For example: factoring 21x5 - 2x2 + 4x - 1, you probably will have to guess and check what goes in the parentheses. It could be (3x - something)(7x + something)(x - something)..., or, it could be something entirely different. Aside from the limited equations like difference of squares, or sum/difference of cubes, I would like to know if it is possible to not have to guess and check. If you do not know of a solution, thank you anyways for your time."
Hi Wesley, In addition to the rules that you mentioned, you can find a few more rules here, including sum/difference of odd powers, sum of even powers, grouping, and something I like to call aggressive grouping.
If none of those help, another tool that might help you out is something called the Rational Root Theorem. The rational root theorem says that if a rational zero to a polynomial exists, then written in simplest form p/q, p is a factor of the constant, and q is a constant of the highest order coefficient.
How does this help in factoring? Well, if p/q is a zero of the polynomial, then (qx - p) is a factor.
It's important to note that the statement above has a big "if" in it. It's possible that no rational roots exist. But if they do exist, this rule helps us out in our trial-and-error search by eliminating possibilities.
Let's take an example: 3x3 - 5x2 - 42x - 40 = 0.
The rational root theorem tells us that if this has rational roots, they are of the form p/q, where p is a factor of 40, and q is a factor of 3. Now, this still gives us a LOT of possibilities to consider, because p could be 1, 2, 4, 5, 8, 10, 20, or 40 (plus the opposites of all of those), and q could be either 1 or 3 (or their opposites).
So let's start with something that's not a fraction: Let's try 1, and see what happens. I'm going to do synthetic division on this. If you don't know how synthetic division works, you'll want to take a look at this explanation: How to do synthetic division.
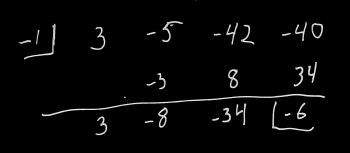
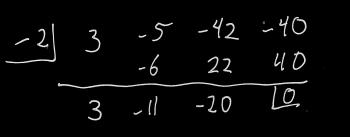
The next bit of good news is that we can use the values in our synthetic division to reduce the polynomial by the factor we just found: our polynomial can be rewritten as (x + 2)(3x2 - 11x - 20) (note the numbers at the bottom of our synthetic division - they are the coefficients of the reduced polynomial). To find our next factors we can use the techniques that we're familiar with on the factor 3x2 - 11x - 20, or we can continue doing synthetic division.
Of course, I cheated; I created a polynomial which I knew could be factored, but there's no guarantee that a given polynomial is factorable over real numbers, let alone rational numbers! Your polynomial, for example, has only one real root, and that one real root is not rational. If you had tried the rational root theorem on this, you would have tried 1, 1/3, 1/7, 1/21, and the opposites of all of those, only to find that none of them work. The good news is that because of the rational root theorem, you KNOW that you're done looking for rational roots.
So there are a few more tools for your arsenal; I hope something here was helpful!
Question: "If I’ve used ninety percent of my hand sanitizer which was seventy percent alcohol, and I refill the bottle with new hand sanitizer which is eighty percent alcohol, what is the new alcohol content of the bottle?"
This is a fairly straightfoward mixture problem. One way of approaching this problem is to begin by writing everything as a percent:
Initailly, the bottle of hand sanitizer was 100% full, then 90% was removed. Thus, we had 100% - 90% = 10%. And 70% of that was alcohol.
Then we filled the container back up, meaning we added (100% - 10%) = 90%. And 80% of that was alcohol.
Thus, the amount of alcohol in the mixture is
10% x 70% + 90% x 80% =
0.10 x 0.70 + 0.90 x 0.80 =
0.07 + 0.72 = 0.79 =
79%
NOTE: If you want to practice doing word problems, the lesson plans section of the site contains a page on mixture word problems. There are worksheets available, and answer keys for pro members.

There's another stunt that has been used recently to promote fake news, and it involves the website archive.org, which is basically an archive of everything that's ever been on the internet. That's right - if you posted a sappy love poem to your childhood sweetheart back in 2001, it's probably still out there, just waiting for someone to discover it in 2020.
There are sites out there (medium.com is one example) which allow anyone to post on their site. In fact, Medium posts a notice that looks like this:
So someone who wants to promote fake news can go to a site like Medium, create an account, and post whatever they want. Now, Medium makes it clear they're not going to fact-check everything, but if enough people complain about an article, they'll run it through their editorial process, and if they find that the article is bogus, they'll remove it. In fact, they'll replace it with a notice that looks like this:
So the fake-news purveyor has wasted his time, right? Not at all! He probably assumed that would happen. That's where archive.org comes in. If his article remained on Medium long enough for Archive to scrape it, it now exists, and will forever exist, as part of the internet archive. So all he has to do is start sharing the version of the article on Archive.org.
So now, when you are scrolling through your social media account, and you see an article that looks interesting, before you click on it, check to see what the source is. "Archive.org" sounds like an impressive source, but if someone is sharing it from the internet archive, it's almost guaranteed that means the article has already failed a fact-check somewhere else.

Have you ever wondered why news sites will occasionally put the word "Report" in their headlines? For example:
Report: Abraham Lincoln Thinks the Internet Is Dumb
or
Alien Spaceship Lands in New York City: Report
These headlines are, of course, a bit silly. But why is the word "Report" in there? Here's an example of why this might happen:
The New York Times does some investigative journalism and discovers that Cinderella is actually as mean and nasty as her wicked step-sisters, and spends her weekends beating up kids at playgrounds and feeding cyanide to pigeons (with all due respect to Tom Lehrer). So they write up a major news article about Cinderella and her weekend habits.
Now someone at CBS catches this story and thinks, "Our readers should know the truth about Cinderella, too!" Unfortunately, no CBS reporter has actually independently verified the details of the story. Under these circumstances, CBS might publish a headline like this:
Report: Cinderella Kills Pigeons
Then somewhere in the article (usually in the first paragraph, but not always), there will be a phrase like this: "according to a new report by NYT..." If it's an online article, that phrase will likely be a link to the original New York Times article.
The addition of the word "report" into the headline does two things for the news site. First, it allows them to acknowledge that they're using someone else's information. But also, it allows them to maintain some deniability. "We're not saying this ourselves, we're just telling you what someone else said," is the implication.
It can be dangerous, because it does allow dishonest sites to get away with all sorts of false reporting. If I can find someone (anyone) who claims that the wicked witch was not planning to eat the children, I can create a headline like this:
Report: Gretel Burns Innocent Woman Alive
In other words, if you are unscrupulous, you can get away with passing off a rumor as a news story.
Fake news sites and Fringe news sites have been using this technique for years, because they understand some very important psychology:
- If you want someone to believe something, put it in the headline, because most who see the headline as they're scrolling through their social media will not click through to read the story. There have been studies done on this: Americans are relying more and more on headlines to get their news. According to an API study done in 2014, less than half of Americans surveyed read past the headlines in the last week. If you think that statistic has gotten better in the last six years, then: "Report: I've got a bridge to sell you."
- Even if they do click through, the headline itself has framed the reader's understanding in such a way that they are prone to accept the reporting as factual, even if it turns out that the source is utterly unreliable. (Check out the following New Yorker article, which examines an APA study on this topic).
For fake news sites, this is a win-win situation. Whether the person reading the headline clicks through to the article or not, their perceptions of reality have been changed. And if they do click through, the fake news site earns money from advertising. I've been watching fringe news sites do this for several years, and they are getting very good at it. Pay close attention to every article you read, and evaluate the reliability of their sources. Resist the temptation to read a headline and scroll on without investigating. If you read a headline, and don't have time to read the article, assume it's not true (particularly if you're not familiar with the source). Once you find a site that regularly uses techniques to pass off rumor as truth, avoid clicking through to their articles - do your part to help dry up their revenue sources.

