Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Here's a fun question regarding an upcoming snowstorm:
"4 to 8 plus 4 to 8 equals 8 to 16, right?"
This is in reference to a prediction that tomorrow there will be 4 - 8 inches of snow, and then tomorrow night there will be 4 - 8 inches of snow. The questioner is suggesting that this means there will be a total of 8 - 16 inches of snow.
It seems reasonable, right? Except we're all pretty sure we're not going to see anywhere near 16 inches of snow in the next 48 hours. So why can't we just add these two ranges together?
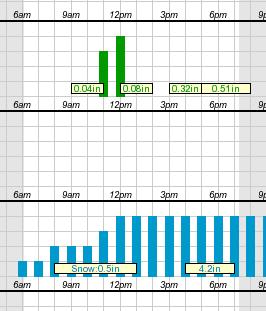
Meterologists have a LOT of unknowns they have to deal with (and I'm not a meteorologist, so I'm not going to pretend I know even a tenth of the variables they deal with). But what I do know is that one of the broad uncertainties is when a storm will pass through. If you look at the chart here (taken from an actual hourly forecast on the National Weather Service website), you'll see that they don't actually know when the storm will start; the snowfall bars begin (with low probability) at 6:00 AM. It's not until noon that they're saying with confidence, "We'll have snowfall by now."
So hypothetically, if the snowstorm starts at 6:00 AM, and goes all day, maybe we'll get 8 inches of snow during the day. But if that happens, the storm will be mostly over by evening, and maybe we'll get 4 inches overnight.
On the other hand, if the storm doesn't start until noon, maybe we'll get 4 inches during the day. But then the storm will last longer into the night, and maybe we'll get 8 inches overnight.
What I've just described is a scenario in which we get a maximum total of 12 inches. But if we were to break it down by how much falls during the day and how much falls at night, we'd have to say "4 - 8 during the day" and "4 - 8 during the night" - even though we feel confident that the storm won't give us more than 12 inches total.
What we're seeing is that a portion of the snowfall could come during the day, and it could come at night. Since we don't know when, it gets listed in both time periods.
Watch the forecasts and see how they line up from storm to storm, and you'll see what I mean: if the daytime forecast is accurate, the overnight forecast will likely be overkill. And vice-versa. Of course, we don't always notice this, because as the storm gets closer, the meteorologists are able to refine their models better.
Then we just whine that the meteorologists have been "hyping up the storms." :D
As I mentioned before, there are undoubtedly many many more variables that I'm not considering, but my purpose here was to show wny you can't just sum the ranges to get a total.
Maizi from Norwich asks, "Four positive whole numbers add up to 84 One of the numbers is a multiple of 17 The other 3 numbers are equal. What are they?"
Hi Maizi, as is my custom with math problems, I'm not going to answer your question; instead I'm going to invent a similar problem and show you the technique for solving it. This will allow you the satisfaction of solving this particular problem on your own. So here is my problem:
Five positive whole numbers add up to 97, and one of them is a multiple of 19. The other four numbers are all equal. What are they?
First, we consider that if we add together four equal numbers, the result must be a multiple of four. For example, 7 + 7 + 7 + 7 = 28, or 11 + 11 + 11 + 11 = 44.
Algebraically, we'd say that n + n + n + n = 4n.
So this means that if we subtract the first number (the one that's a multiple of 19) from 97, we will have a result that is a multiple of 4.
What could the first number be? 19, 38, 57, 76, or 95. Any other value is larger than the sum of 7, which is not possible if all the integers are non-negative.
Based on this, we can find all possible sums of the other four numbers, by subtracting each of the numbers above from 97:
97 - 19 = 78
97 - 38 = 59
97 - 57 = 40
97 - 76 = 21
97 - 95 = 2
Remember what I said earlier? The other four numbers must add to a multiple of 4. The only one of those sums above that is a multiple of 4 is 40. Therefore, we conclude that the first number is 57, and the other four numbers are each 10 (because 40 / 4 = 10).
I hope that's helpful; good luck with your version of the problem!
Rosanna from Italy writes, "I'm an Italian student of English, dealing with learning literature. Introducing the Medieval ballad, after analysing Lord Randal, we're analysing Geordie, the English version. Our book text introduces the counting of stressed and unstressed syllables in medieval ballads but the answer seem to get me confused because it is said that there is a mixed of four and three stressed syllables lines without indicating the lines. Can you tell me what the lines are, what the stressed and unstressed syllables are and if we can specify if they are iambic or anapest feet? Thanks in advance, I really need your help!"
As I walk’d o’er London Bridge
One misty morning early
I overheard a fair pretty maid,
Was lamenting for her Geordie.
"O, my Geordie will be hang’d in a golden chain,
’tis not the chain of many,
He was born from King’s royal breed
And lost to a virtuous lady."
Go bridle me my milk-white steed,
Go bridle me my pony,
I will ride to London’s Court
To plead for the life of Geordie.
"O Geordie never stole nor cow, nor calf,
He never hurted any,
Stole sixteen of the King’s royal deer
And he sold them in Bohenny.
"Two pretty babes have I born,
The third lies in my body,
I’d freely part to them ev’ry one
If you’d spare the life of Geordie."
The judge look’d over his left shoulder,
He said, "Fair maid, I’m sorry,
So, fair maid, you must be gone,
For I cannot pardon Geordie."
O my Geordie will be hang’d in a golden chain,
’tis not the chain of many,
Stole sixteen of the King’s royal deer
And he sold them in Bohenny.
Hi Rosanna, you've got an especially interesting poem to decipher. Ballads are made challenging by the fact that they were originally intended to be sung rather than spoken. Song-writers often feel like they have more flexibility in their writing than poets who intend their poems to be spoken. The reason for this is that it's easier to cram extra syllables into a song; all you have to do is take a quarter note and change it into two eighth notes, and you've put an extra unaccented syllable between your accented syllables.
To see this illustrated, a good starting point is to find an audio recording of the ballad and listen to it. Here's one I found. The lyrics are not exactly the same as the copy you sent me, but they're fairly close. Geordie Ballad on YouTube.
One of the best lines to hear this "syllable cramming" that I mentioned above is the first line of the repeated chorus in the video:
"He never stole a cow, never stole a calf"
When you listen to that line, you can hear that the singer is really working to fit extra syllables in. In particular, "stole a" in the first half of the line and "never" in the second half are jammed together to make the line of music flow. If you focus your attention on what syllables get accented here, what you'll hear is:
'he NEV-er stole a COW, nev-er STOLE a CALF"
Interesting, isn't it, that the first time the word "never" shows up it has an accented syllable, but the second time it shows up, the entire word gets jammed into the space between two accented syllables. This sort of thing makes poetry both interesting and challenging!
If I were going to break this down by accented and unaccented syllables, I might replace each unaccented syllable by a lower case "x" and each accented by an exclamation mark. It would look like this:
x ! x x x ! x x ! x !.
This doesn't seem terribly helpful; the number of unaccented syllables does not stay consistent throughout the line. However, at the very least we can tell that there are four accented syllables in this line. Now let's look at the next line:
"He never murdered any."
This one is much more straightforward, and if you just simply read it aloud, you would hopefully hear the natural rhythm of it:
"he NEV-er MUR-dered AN-y"
So this one is: x ! x ! x ! x, which has three accented syllables.
The next line is "STOLE six-TEEN of the KING'S ro-yal DEER" , which is: ! x ! x x ! x x !.
And finally: "and he SOLD them IN bo-HENN-ey" or: x x ! x ! x ! x.
Let's put it all together to make an accent "map" of the chorus:
x ! x x x ! x x ! x !
x ! x ! x ! x
! x ! x x ! x x !
x x ! x ! x ! x
If you count up the exclamation marks in each line, you'll find that the pattern for the number of accents in each line is 4 - 3 - 4 - 3, which answers the first part of your question.
Now to answer whether it's anapestic or iambic (or something else altogether), I looked at the second line and noticed that it is almost perfectly iambic (unstressed, stressed), except for the extraneous unaccented syllable. On the other hand, the very next line is missing an unaccented syllable at the beginning, which makes up for it. So my money is on this being iambic heptameter (because a line of four and a line of three add up to a total of seven iambs). To convince myself that I'm right about this, I go back and listen again, and everywhere I hear the singer doing "syllable cramming", I replace the crammed syllables with a single unaccented mark:
x ! x ! x ! x !
x ! x ! x ! x
! x ! x ! x !
x ! x ! x ! x
Aside from the fact that we have two lines that end with an extra unaccented syllable, this is iambic.
So now that you know this is a very "loose" iambic heptameter, you can go back to your version of the ballad, feeling confident of what the meter is. Your only challenges, then, are determining which syllables get stressed, and figuring out where the "syllable cramming" happens. Good luck!
Incidentally, as a side note, I think that the addition of those unaccented syllables at the end of each pair of lines gives it a sense of being unfinished, which adds to the melancholy feel of the piece.
After a few back-and-forth messages with Rosanna, here are a few more helpful tips for people trying to parse accented/unaccented syllables in a poem:
- Once you think you've figured it out, read it out loud, strongly emphasising (speaking loudly) the syllables you marked as stressed. This may help you identify mistakes you've made.
- If you know how many stressed syllables there are supposed to be in each line, that's very helpful information, because while a poet may mess with the unstressed syllables, they're less likely to change up the number of stressed syllables.
- You're unlikely to find two stressed syllables in a row.
Michelle from Maine wants an explanation of the difference between linear-scale graphs and logarithmic-scale graphs. Her question relates to coronavirus infections and COVID-19 deaths, so I'm going to use COVID-19 data in my answer.
For this explanation, I'll going to use the data for US coronavirus infections, from March 10, 2020 to March 31, 2020. That data is shown below. The data was obtained from Worldometer stats from April 1, 2020.
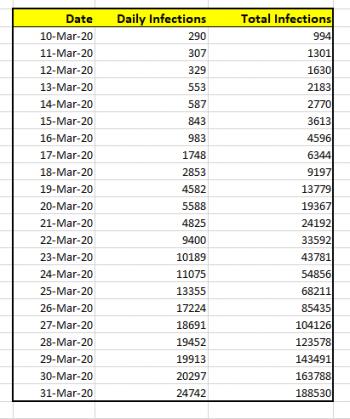
If I wanted to simply chart the total number of cases against the date, the graph would look like this:
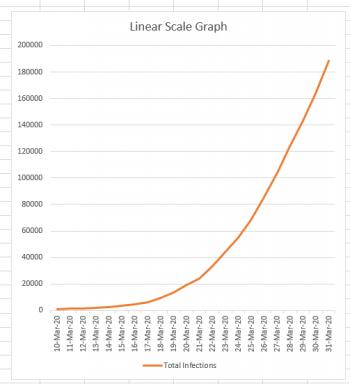
Now, this graph looks a bit scary, because it's clear from this graph that the number of cases is skyrocketing very quickly. And this is the nature of an exponential curve. If we could continue this graph a month into the future, and the growth remained as it currently is, it would still have roughly the same appearance, except that instead of the March 31st data being at the top of the graph, it would be down near the bottom because the new numbers would completely dwarf it.
It's important to know that in recent days this is not the graph which has been making the rounds on social media and in news articles. Mathematicians (and scientists) have a different type of graph we like to use when we're dealing with exponential curves: it's called a logarithmic scale graph. In a logarithmic graph, we keep the x-axis (the date values) the same, but we do some "squishing" of the y-axis. How do we perform this squishing?
Logarithmic Squishing
Normally if you were drawing a graph on a piece of graph paper, you would say, "Each square is worth 1 unit," or "Each square is worth 100 units." But regardless of what you decided, you would consistently consider each square to be worth the same amount. You can see that this is what we've done in the linear-scale graph above. Each horizontal line marks off the same amount: if you go up one line, you've gone up 20,000 infections. That's true at the bottom of the graph, and it's also true at the top of the graph. (200,000 - 180,000 = 20,000).
But if you're drawing a logarithmic graph, each square height has a different value depending on how far up the graph it is. If the first square is worth 1 unit, the square above it is worth 10 units, the square above that is worth 100 units, and the square above that is worth 1000 units. You can see what's happening, right? Every square is worth TEN TIMES as much as the square below it. The result is that the entire graph gets squished. For mathematicians and scientists it's a great way to get a lot of data into a single graph. This is what our data looks like when it's graphed this way:
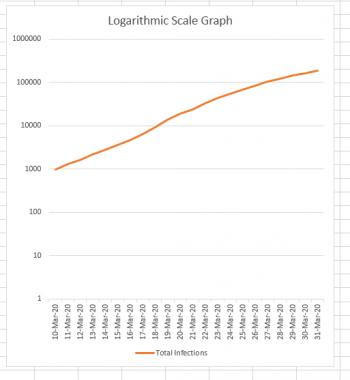
Notice how the difference between the first two horizontal lines is 10 - 1 = 9 infections. The difference between the next two horizontal lines is 100 - 10 = 90. Continuing on to the top, we see that the difference between the last two lines is 1,000,000 - 100,000 = 900,000.
It's really, REALLY important to understand that the two graphs above are actually BOTH SHOWING THE SAME DATA, just in very different ways.
Logarithmic scale graphs can be very useful; if a graph is exponential, its logarithmic counterpart will be a straight line. The slope of that straight line (how steep it is) helps us understand how quickly the graph is rising. It basically becomes a rate-of-change graph, which is why most news sites that are showing multiple states/countries in the same graph are using a logarithmic scale. Comparing the logarithmic graphs lets us see more easily which states/countries are doing better/worse at containing the infection. If the logarithmic graph for New Jersey is steeper than the logarithmic graph for New York (which it currently is) that helps us to understand that the infection is spreading more rapidly in New Jersey (even though the number of infections in New York currently VASTLY outnumbers the New Jersey infections).
The Danger
The danger, of course, is that most people don't really understand the difference between a linear-scale and a logarithmic-scale graph. So when we repeatedly see logarithmic graphs, it's easy to get fooled into thinking that the growth is linear, when it's actually exponential. If you are looking at a news site that shares graphs of infections (or deaths) look for an option to go in and out of logarithmic mode. Look at the data in BOTH modes, now that you understand why the modes exist. The linear-scale graph gives you reality, while the logarithmic-scale gives you a mathematical tool for comparing rates of growth.
Jon from California hopes that I can explain why total population of a country doesn't "matter" to infection spread.
Jon's question stems from a very common issue - many people will argue that if we are going to compare one country's coronavirus infection with another country's, rather than comparing total cases, we should be comparing the infection percent. It's easy to see why people from the United States want to make that comparison; the United States has a massive population, so if we look at percentages, it makes it look like we're actually "doing better" than much smaller countries. In fact, I've seen people sharing graphs like this one below (click the image to view it at full size):
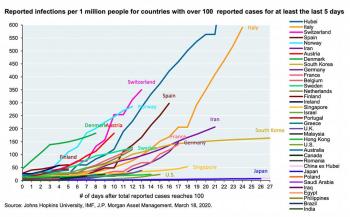
If the only thing you see is this graph, you're going to assume that the United States is doing better than just about every country out there. So let's look at the math and see why this graph - while it makes us feel good - doesn't actually provide the full picture.
The Thief Analogy
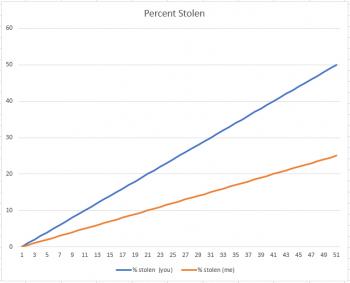
Suppose you have $100 and I have $200. A thief comes along and says, "For the next fifty days, I'm going to steal $1.00 from each of you each day." I might say, "I'm better off than you, because he's stealling 50% of your money, and only 25% of mine." And I'd be right, as the graph below shows:
But now suppose the thief came to us and said, "I'm going to steal $1.00 from each of you indefinitely." Now, all of a sudden, I'm not interested in comparing my percent with yours. Why? There are two reasons. First, I have more money to be stolen, and second, the only difference between you and me is that it's just going to take longer for him to take all my money. But in the end, the graph will look like this:
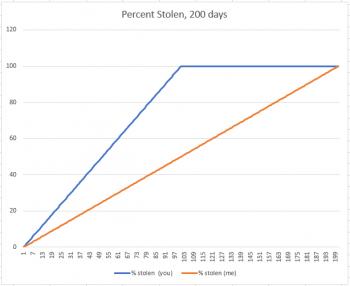
Your percent stolen increases until it reaches 100%, and then it sits there at 100% until my percent matches yours. You've lost $100, because that's all you had, and suddenly the fact that I used to have $200 only means that I lost 100 dollars more than you did.
What's the difference between the two scenarios above? One is a closed situation, and the other is open-ended. As long as we put an end date on the thievery, I feel good about having a bigger "money population" than you do. But if it becomes open-ended, that doesn't actually matter anymore.
The Apple Analogy
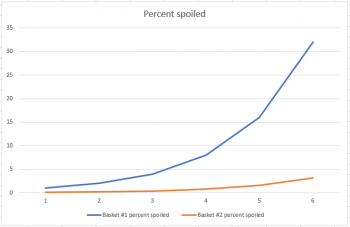
Suppose you have two baskets. One has 100 apples, and the other has 1000 apples. Each basket has one rotten apple. And every day, any rotten apple turns one other apple rotten. If we think of this as a percent population problem, and just look at the first six days, it definitely looks like basket #2 is doing better:
But if we extend the graph from six days to eleven days, we get a much different picture:
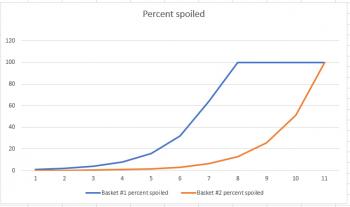
This example works out just like the thief example; the short-term graph is deceptive, but the long-range graph let's you see how the situation ends. The primary difference is that, like a virus, the apple example is exponential in nature, so the graphs share a similar shape to the ones related to coronavirus.
But...
Infection Rates Don't Work Quite Like This
Viral infections don't work exactly like this. For starters, an apple will never recover from rot, and therefore it will never become immune to rot, and never stop passing on the rot. Thus, it is guaranteed that eventually rot will reach all 1000 apples.
But with an infection, people do recover, and when they do recover, they become immune, and cease to be carriers.
Why does this matter? Suppose that you have a sickness, and on any given day you have a 10% chance of infecting each person you interact with. Let's also suppose that on average, you interact with 100 people. This means that you'll likely infect 10 people on the first day. The next day, you interact with another 100 people, and infect 10 more. The next day, you interact with 100 people, but because you (and others like you) have been spreading infection, some of those people (let's say 10 of them) are already infected. Since there are only 90 people you can infect, you'll end up infecting 9 people instead of ten.
If half the population becomes infected, 50 out of your 100 people have already been infected, so you'll only infect 5 more.
Eventually the massive spread of the sickness will meet head on with a dearth of new people to infect, and the infection rate will stop increasing. In math we refer to that as an inflection point. It's the point where the rate of increase begins to decrease (if you can wrap your brain around that idea!). In case you care about the deeper mathematics of the situation, an inflection point is where the second derivative goes to zero and then changes sign.
The mathematical term for this kind of growth pattern (you'll see example graphs below) is a logistic curve.
And here's where things get complicated, because the inflection point doesn't just depend on the virus - it depends on MANY factors, including us, and our behavior. If I, as an infected person, stop interacting with 100 people every day, and instead interact with only 5 people, I've changed how the sickness spreads.
But all other things being equal, the inflection point is primarily based on population. If there are only 1000 people for me to interact with, everyone is going to very quickly start interacting with the same people over and over. But if there are millions of people, the infection can spread to many many more people before we reach the point that I'm mostly interacting with people who have already been infected.
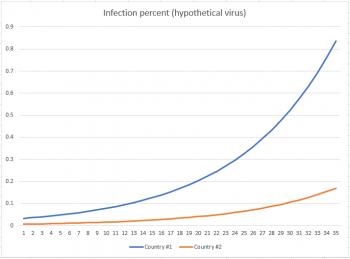
I invented a hypothetical virus (emphasize hypothetical - this is NOT coronavirus) which reaches its inflection point at around 20% population before the infection rate starts to decrease. I also created a graph showing % infected for two countries: one with a population of about 60 million, and the other with a population of about 300 million. My first graph shows how things stand after 35 days. You can see clearly that, as a percentage, country #2 (the one with a massive population) is doing far better than country #1, which already has almost 1% of its population infected.
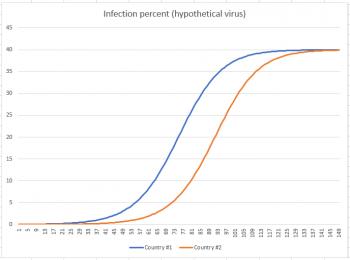
But now fast-forward to Day 150. You can see from the graph below that at approximately Day 73 country #1 hit its inflection point, and country #2 hit its inflection point about 20 days later. By the time we reach Day 150, both countries have settled down to about 40% of their populations infected.
So now that we've seen where this situation takes us, let's take that last graph and remove the percentage calculation from it, so we can see how it affects total population. The graph below shows infections in 10,000s of people.
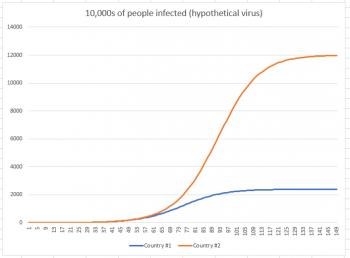
While country #1 appeared to be doing much worse in the first graph (because we were looking at a short-term graph), once we extend the graph to its conclusion, we see that in reality, country #2 had far more infections. Country #1 had 24 million infections, while country #2 had 120 million. Why did country #2 have so many more infections? Because the infection had more people to work its way through. Just like the thief had more dollars to work through, and the rot had more apples to work through.
People may tell you that comparing the number of infections in one country to the number of infections in another country without regard to population is like comparing apples to oranges. Instead, as you can see here, comparing percentages is the comparison that is apples-to-oranges. It may make you feel good in the short term, but feeling good about the short term without considering the long term is actually a short-sighted way to view the world.
As an addendum to this, it's worthwhile to note that there is a time when the percent graph is very informative: when the disease has run its course. At that point, we will look at the total population numbers and certainly grieve over each loss of life, but we will also look at the percentage graph. Not all countries will have halted the disease at the same population percentage, and when all the numbers are in, those percentages will be meaningful. The data will help us understand how we did in comparison to other countries. Not to gloat or grieve, but rather, to help us understand what measures were effective and which were not, so we will be better prepared next time.

