The following blog post is an example problem designed to show why I don't answer peoples' "Matchstick Problems" on this blog. We've set up a new "Codes and Riddles" forum on our Community Forum, so you can share your matchstick riddles there and ask for help solving them. In order to post in the forum you must have a free membership account (click the login link at the top of the page to get started). We have an unusual "CAPTCHA" for the forum - instead of typing letters to prove you're human, we require you to solve at least 5 puzzles on the site before you post anything. (Here's a hint: Blackberry Game is about the simplest game on the site, so you can rack up your 5 games easily there!)

You wouldn't believe the number of times people have contacted me to ask me to solve a matchstick problem for them. You know the kind of problem I'm talking about, right? You're given a layout of matchsticks, and you are asked to move two (or one, or three, etc) matchsticks to form the largest number possible.

Here's an example: move 4 matchsticks to make the largest number possible out of the following:

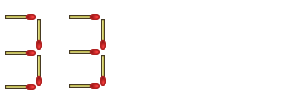
And to this second complaint, I reply, "Of course I moved four! I picked up two others and set them back down again!"

"That's not allowed," you say.

"Fine," I reply. "I didn't just set them down; I swapped them."

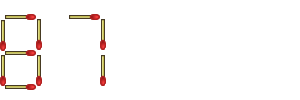
Here's a better solution, which, in a literal sense, thinks outside the box - instead of limiting myself to the two digits given, I expand the number to the right. This is a fairly obvious solution, and you shouldn't have any complaints about it:

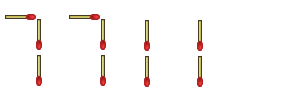
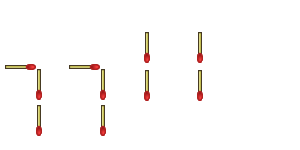
"There," I say, "that's about 500 quintillion - beat that!"

"You cheated! I never said you could use exponents!"

"And you never said I couldn't," I reply.

But wait! Who says a number one has to be two toothpicks tall?  Aren't they still ones if they're made out of one matchstick apiece? Couldn't we do this:

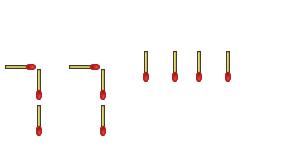
"Cheater!" someone declares, "You can't change the structure of the numbers!"

"I haven't changed the structure." I reply. "Exponents are supposed to be smaller, so I've formatted it perfectly."

Are we done yet? Are there more ways of thinking outside the box? Sure! Take a look at this one:

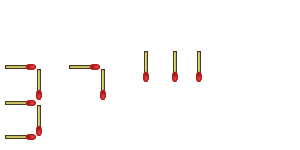
"Yeah, but you knew it was a seven, didn't you?"

"Besides," you protest, "you only moved three matchsticks - you couldn't have swapped two others, because that would have meant moving FIVE matchsticks"

"Ah," I say, glad to have you distracted from my malformed seven, "I picked up one that I wanted to move, and one that I didn't want to move, placed the one I wanted to move to the position of the one I didn't want to move, and then moved that one to the new position."

"Okay, fine!" you say, "You win!"

So what is that number? Well, we need to evaluate 7¹¹¹ first, and that's 3.9e93, and when you try to raise 3 to that number, you're going to get an overflow error on your calculator.

And so I sit here smugly satisfied with myself - until someone else comes along and says, "Wait a minute! If you're going to let him get away with that malformed 7, then I can do this:"

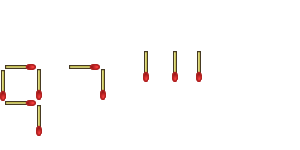
No! Even though I've come up with solutions that are too big to run through your calculator, this is just what I came up with on the spur of the moment - there are almost certainly better solutions out there! *

So what's the point? The point is twofold:

1. Have fun with these kinds of problems, but if someone asks you one of these and doesn't clarify the rules of what you can and can't do, just have fun thinking outside the box, and when they say, "You can't do that!" enjoy the opportunity to annoy them with the response, "You never told me I couldn't!"
2. If you ask me to solve your matchstick puzzle, I will simply direct you to this blog post, because I would almost certainly NOT come up with the solution the problem poser was looking for, so why should I even try - it's not MY puzzle after all! :D

Happy Puzzling!
Professor Puzzler

* Within a half an hour of posting this, two more even better solutions popped into my head - neither of which require malformed numbers.  How many can you find that beat 9^(7^111)?