Seventh grader Colton from Florida asks, "If triangles have the same area, are they similar? Or do triangles have to have the same perimeter to be the same? I think it's area. Thank you "

Hi Colton! 

Thanks for your question. I want to make sure we're talking about the same thing here. In one question you talk about triangles being "similar" and in the next you talk about them being "the same." These are two very different questions, that use very different concepts.

You see, triangles could be congruent (what you might have meant when you said "the same") or they can be similar.

So what is the difference?

Congruent means that two triangles are identically shaped. The have the same shape and the same size.  They have three pairs of sides that are the same length, and they have three pairs of angles that are the same measure. We call the pairs of parts "corresponding parts," and we say that in congruent triangles, "Corresponding parts of congruent triangles are congruent" (which gets shortened, often, to "CPCTC").

Another way of saying that: if you have two triangles that are congruent, you could pick one of them up and set it down on top of the other, and they would match perfectly. You might have to flip or rotate the one you picked up, but if you can't make it line up perfectly on the other triangle, they aren't congruent. In the image below, the triangles are congruent, because you could pick up the one on the right, rotate it about 45 degrees counter clockwise, and it would fit exactly on top of the triangle on the right.

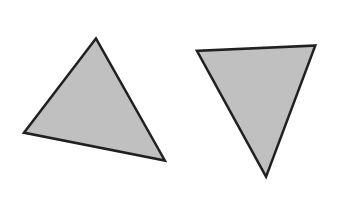
As for your question: if two triangles have the same area, are they congruent? Not necessarily! I can create two triangles that take up the same amount of space, but have very different shapes. And the same is true of perimeter; just because two triangles have the same perimeter, that doesn't mean they're the same shape.

There are ways to tell if two triangles are congruent. For example, if you have two pairs of sides that are the same length, and the pair of angles between those sides is congruent, then it's guaranteed that the two triangles are congruent. Maybe in another blog post I'll explore all the different congruence theorems!

But now we need to consider similarity. Similarity is different from congruence. Two triangles can be similar without being congruent. Two triangles are similar if they have the same shape, but not necessarily the same size. What do I mean by "same shape?" Well, one way of explaining it is to say that all of their pairs of angles are congruent. 

Or, imagine that you have two similar triangles printed on transparencies. You might not be able to lay one on top of the other so that they match, but if you hung one of them on the wall, and used a projector to project the other one onto the wall, you could make them line up by getting the projector the right distance from the wall.

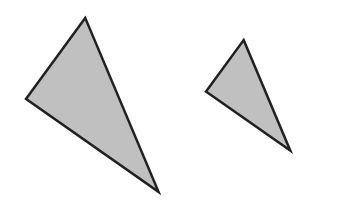
This picture is an example of two triangles that are similar. You can see the shape is the same; they both have two smallish angles, and one bigger angle. You couldn't lay one of them on top of the other and have them match perfectly, but if you expanded the smaller one, you could make it fit perfectly on the larger one. They are similar.

Okay, so now we come back to your question: if two triangles have the same area, or the same perimeter, are they similar? Not necessarily! You could have two triangles with the same perimeter (or the same area) that aren't the same shape at all. And if they're not the same shape, they're not similar!

So, in conclusion, neither the area nor the perimeter will help you determine if two triangles are similar, or determine if they are congruent!

That's a pretty long answer to a short question, but hopefully you learned some important concepts along the way.

Thanks for asking your question, Colton.

Sincerely,
Professor Puzzler