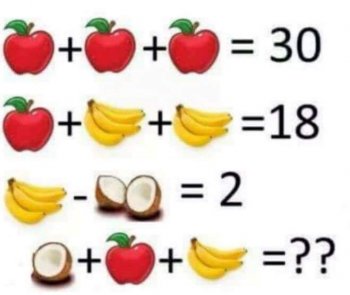Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
The question of the day is:
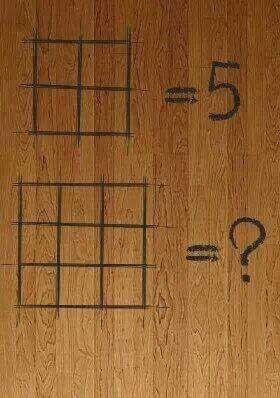
Can you solve it? If you said "yes," Then you are probably wrong. This is really not a "solvable" problem. It was created by someone who wanted to generate arguments and disagreements, because arguments translate into attention, likes, and shares.
You see, it's pretty much impossible to draw conclusions about a pattern when you only have one example from which to draw your conclusions. Depending on what pattern you notice, there are a multitude of "correct" answers.
I think the most common conclusion is: 5 is the number of squares in the image (four little ones and one big one). If this was your interpretation, then the answer is 14 (9 little squares, four medium squares, one large square).
However, there are other ways of interpreting the image. 5 is the number of line intersections involving interior line segments. In which case, the number for the second image is 12.
Another way of looking at it: 5 is the number of squares which border on the edge of the diagram. In which case, the answer to the second diagram is 13 instead of 14, because one of the squares (the central little square) doesn't border on the edge of the diagram.
But we don't have to stop there - as Brian Twitchell (District Math Coach, RSU #74) points out, we can create even more patterns:
- If we take one less than the number of horizontal unit segments, we end up with an answer of 11.
- If we take seven less than the sum of the number of horizontal and vertical unit segments, we get an answer of 17.
- Forget unit segments; consider line segments that span the length/height of the diagram. Now subtract one. This also matches the original diagram, and gives an answer of 7.
So don't be too quick to assume you have "the" answer to a question!
If you enjoyed this post, you might also be interested in Professor Puzzler's analysis of this sneaky problem: