Sixth grader Abdulla from U.A.E. asks the following question: "Are there perpendicular sides in trapezoid?"

The answer to that question, Abdulla, is "sometimes yes, sometimes no."

When people say the word "trapezoid," the image that automatically conjures up for most people looks like this:

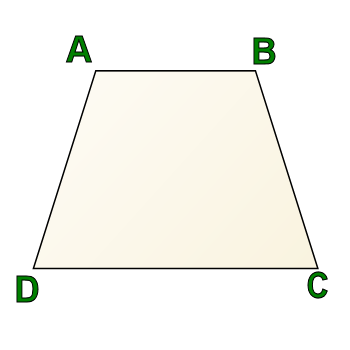
This is a trapezoid, and it is often described as a triangle with the top lopped off, or as a "dog food dish."

In this particular trapezoid, there are no perpendicular sides. A and B are both obtuse angles in this diagram, and C and D are both acute angles.

However, not all trapezoids look like this. Let's talk for a moment about the definition of a trapezoid.

Interestingly, the definition of "trapezoid" will vary depending on the part of the world in which you live, and in some parts of the world, the word "trapezium" is used for what I refer to as a trapezoid. I'm going to show you two definitions of trapezoid, and you'll need to check with your teacher/textbook to find out which way of defining a trapezoid is used in your part of the world.

Definition A: A trapezoid is any quadrilateral with exactly one pair of parallel sides.

Definition B: A trapezoid is any quadrilateral with at least one pair of parallel sides.

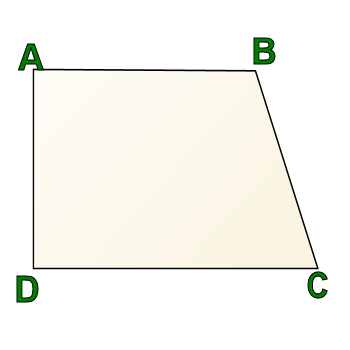
Regardless of which definition you use, the following is a trapezoid:

AB is parallel to CD still, so it meets definition B, and since AD is not parallel to BC, it also meets definition A.

This trapezoid is called a "right trapezoid." Why? Because always true of trapezoids (regardless of your definition): Right angles come in pairs in a trapezoid.

Why? Because

So this answers your question: Yes, some trapezoids have perpendicular sides.

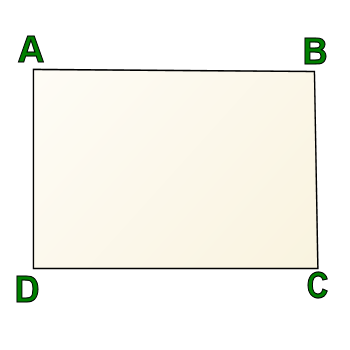
Let's take this one step further, though. Here's another figure. In this one, you have four right angles. That makes this a rectangle.

But is this figure also a trapezoid? It depends on whether you're using definition A or definition B.

If you're using definition A, it absolutely is not a trapezoid, because it has two pairs of parallel sides.

However, if you're using definition B, having two pairs of parallel sides is okay.

So if you're using definition B, then a trapezoid could be made up entirely of right angles, and a rectangle would be a special kind of trapezoid.

Otherwise, if you're using definition A, the most a trapezoid could have is two right angles, and therefore, two perpendicular sides.

Hope that helped answer your question!

Professor Puzzler

Open up a flexible tape measure, until the year of your birth (last two digits) plus 100 is showing. Now bend the tape measure over and bring back the end of it until it lines up with your birth year. Now find the last two digits of the current year, and see what corresponds to it on the other side of the loop you've created. Take the last two digits of that number and subtract it from 100 and you'll have your age. Why does this work?

First of all, let's start by setting some limitations on this, because it doesn't always work. A couple towns over from us there is a woman who just turned 106. If we try this trick for her age, we find out that she's 6 years old. So if someone is over a hundred, we have to use a little common sense and say, "Well, she doesn't look like she's 6 years old, so we'll add 100 to that."

So in exploring this, we'll ignore any age 100 or more.

Also, we need to agree that we're talking about "age at the end of this year," because if the person hasn't yet had their birthday, this trick is off by one year.

With those things clarified, here's an example. My grandmother was born in 1916, so I'm going to fold over the tape measure to look like this.

If I scan back up the tape measure until I find the current year (2015), I find that the number across from it is 101. Now I take the last two digits (01) and subtract that from 100, getting 99 (which is my grandmother's age).

Let's stop for a minute and think about what we've done. We have a total of 116 inches extended on the tape measure. What significance does that number have? 

Let's define some variables and see if we can make some sense of how that number is going to play into the tape measure game.

Since the birth year is the current year minus the age,

(100B_f + B) = (100C_f + C) - A

Let's do a little algebraic manipulation on this equation, rearranging terms until C - B is by itself.

C - B = A - 100(C_f - B_f) 

On the left side of the tape, I see the number B + 100. On the right side, I see 0. Since the left side is increasing from top to bottom, and the right is decreasing from top to bottom, every time I move up a number on the right, I'm moving down a number on the left.

Thus, if I move up to C on the right, I'm decreasing the value on the left by C, giving me: B + 100 - C.

Let's take that B + 100 - C and rearrange it:

100 - (C - B)

Since we found C - B in a previous equation, we can substitute this:

= 100 - [A - 100(C_f - B_f)]

= 100(C_f - B_f + 1) - A

Since we're only looking at the last two digits of the number, we can do a bit of modulus (remainder) math*, and say that 100(C_f - B_f + 1)  is congruent to 100 (mod 100), and therefore, what we're looking at is:

100 - A.

What happens if you subtract that from 100?

= 100 - (100 - A)

= 100 - 100 + A

= A (Current age!)

And there you have it. That's the algebra behind why this trick works.

As an added bonus, the trick also works if you just slide the tape measure out to the birth year, instead of 100 more than the birth year. BUT now we have the stipulation that it doesn't work if we haven't extended enough to get the current year on the right-hand side of the tape measure. So we could say, "Slide the tape measure out until the current year is on the right, and then keep sliding it until the last two digits on the left match the birth year." This saves you having to go out an extra 100 inches in many cases.

* This step of doing some modulus math is the reason the trick doesn't work for people over the age of 100; what we're actually finding is their age mod 100, or the remainder when their age is divided by 100. This has the effect of returning only the last two digits of their age.

Curtis asks us for an explanation for how to do a factor tree.

If a number isn't prime, then it can be written as a product of prime numbers. This product is called the "prime factorization." It's very useful to be able to find the prime factorizations of numbers, because that will help you determine things like the greatest common factor (GCF).

A factor tree is an easy way of finding the prime factorization of a number. So let's do a factor tree example. Let's say we want to find the prime factorization of the number 1,260. First, we ask ourselves, "Is there a pair of numbers that multiply together to make 1,260?"

That question has a lot of answers: 1,260 is 2 x 630, it's 3 x 420, it's 5 x 252, etc. When I did this, the first pair of numbers I spotted was 10 and 126. After all, if a number ends in a zero, like 1,260 does, we know it has to be a multiple of 10. So I drew a pair of arrows coming out of 1,260, and wrote 10 and 126 under the two arrows like this:

I could have picked any of those other pairs, and it also would have worked fine.

Now that I've done this, I need to ask myself, "What is a pair of numbers that multiplies to 10?" and "What is a pair of numbers that multiplies to 126?"

For ten, I came up with two and five, so I drew arrows coming out of 10, and wrote two and five under them.

For 126, I came up with 7 and 18, so I drew arrows coming out of 126, and wrote 7 and 18 under them.

As I'm writing these, I realize that 2, 5, and 7 are all prime numbers (they can't be split up any more) so I draw circles around them.

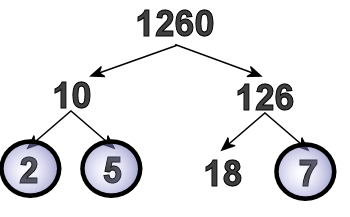
Some teachers, instead of having you circle the primes, will say, "Draw one arrow straight down from the two, and write two under it, so you keep bringing that two down to the bottom." Either way, you need to make sure you don't lose track of those prime branches!

Eighteen can split into factors; I chose to do 2 and 9. (I could have done 3 and 6 instead). So now it looks like this:

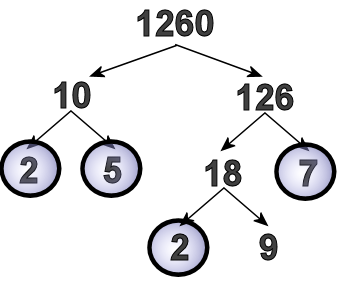
We're almost done, because we've just got one number to split up (2 is prime, so we circle it, and then we just have to deal with the 9.) 

Nine is three times three, so we make our arrows, and write two threes.

Since the threes are also prime, we'll circle those, and our prime factorization looks like this:

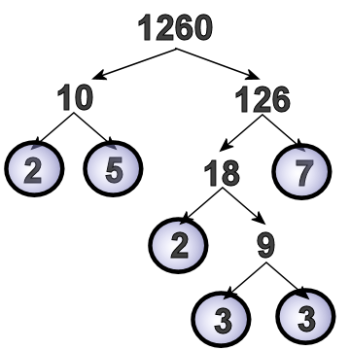
Now that we've split 1,260 up into prime factors, we can say that 1,260 = 2 x 5 x 2 x 3 x 3 x 7.

But it would be better to write each prime factor only once, using exponents: 1,260 = 2² x 3² x 5 x 7.

Hope that's helpful!

Professor Puzzler

Eighth grader Sandesh asks, "consider y=x*x*x*x*x*...... up to infinity . hence y=x*y which means either y=0 or x=1 how can we explain it?"

First, you need to understand that what you're talking about is called a LIMIT. We can't actually multiply x times itself an infinite number of times, because there isn't enough time in the universe to do that!

What we can say is that we're going to multiply x by itself n times, and n is a really really big number. In fact, we say that n is "approaching infinity."

Now, some things have limits, and some things don't. For example, consider this:

1/2 x 1/2 x 1/2 x ...

If we multiply 1/2 times itself a billion times, we get something really close to 0, and if we multiply it a billion and one times, we get something that's even closer to zero! And if we keep multiplying, we get closer and closer to 0. So we say the LIMIT is 0, or that it converges to zero.

On the other hand, consider this:

2 x 2 x 2 x 2 x ...

If we multiply 2 times itself a billion times, we get an astronomically huge number. But if we multiply it a billion and one times, we aren't getting closer to any particular number, we're just getting even more astronomically huge. So this doesn't really have a limit. We say it diverges.

So, I think the important thing you're missing here is that x * x * x * x ... is only convergent for certain values. it converges if x is between 0 and 1 (inclusive). Otherwise it is divergent. (It's divergent for x < 0 because the product keeps flopping back and forth between negative and positive each time you multiply, so it never settles in on any one value. It's divergent for x > 1 because the product explodes to astronomically large values).

And if it's DIVERGENT, then you aren't allowed to do your cute little substitution. However, if the expression does converge (x is between 0 and 1) then your substitution is a useful way of looking at it. (There are more precise ways of looking at it, that you'll learn someday when you take a calculus class, but this will be sufficient for now).

Here's why your substitution won't work in all cases:

The original equation is: y = xⁿ, where n is approaching infinity.

Rewrite it slightly: y = x * x^{n - 1}

x^{n - 1} is the part you want to replace with y.

You see, what you're really doing when you substitute is, you've assumed that "the limit as n approaches infinity of x^{n - 1}" is the same as "the limit as n approaches infinity of xⁿ". But this is only true if xⁿhas a limit! When xⁿ has a limit, then you can do your substitution:

y =xy.

y - xy = 0
y( 1 - x) = 0
y = 0 or x = 1

And this is actually the correct result, for the situation when xⁿ has a limit. Because if xⁿ has a limit, x must be between 0 and 1. If x is any number LESS than 1, then when you multiply it by itself a billion times, you get something really close to zero. We say that its limit is 0. And if x = 1, then y = 1 as well, both of which fit your solution.

The entire study of limits is much more complex than I've made it seem here; I've done my best to keep the math and the terminology fairly simple (hopefully I've succeeded in that!). When you get into a Calculus or Pre-Calculus class, you'll find that there's a lot more to it, but hopefully that'll at least whet your appetite for more!

Professor Puzzler

3rd Grader Adeeb from Canada asks, "Why did you create this game?"

Well, Adeeb, you might not have realized it, but there are lots of games on this site! In fact, there 16 math games, 15 word games, 13 strategy games/puzzles, plus a whole lot of other games, quizzes, and puzzles. So if you thought there was just one game here, you should definitely look around a bit, and see what else you can find!

In general terms, the reason I created this site with all its games, is because I wanted to provide something that would be helpful to teachers and their students. At first (about 13 years ago, when I created the site) there was a bunch of math problems, and just one or two games (Hangman was the very first game I created for the site). For a few years, I got busy with other things, and didn't spend any time paying attention to what was happening at this site.

Then, one day, I came back to look at the site, and was astounded to see that there were about 1,000 people visiting the site every week, and I had no idea so many people were finding the site useful.

At that point, I decided it was time to add more to the site - after all, if people thought Hangman was useful, wouldn't they find a lot of other games and puzzles useful, too?

So over time I kept building and building. Teachers would send me ideas, friends would suggest even more ideas, and a lot of people helped to test out the new games whenever something new showed up on the site.

Now the site is so big I don't even know how many pages it has! Two years ago we started a big redesign of the site that allowed teachers to create their own mazes, puzzles, math problems, quizzes, and more, so the site continues to grow, all the time!

And the number of people who visit the site every week continues to grow...we used to be at around 1,000 visitors per week, but now we get more than that in one day! We usually have about 15,000 visitors every week.

I hope that helped answer your question, and I hope you have fun discovering more games on the site!

Professor Puzzler