Merry Christmas! A couple years ago I mentioned here that someday I would post instructions and templates for creating various ornaments out of cardstock and/or photo paper. Considering we're just days away from Christmas, some parents may be looking for fun activities to do with their children to pass the time on their way to the most anticipated day of the year, so I have put those plans online at last!

We have a whole "Paper Craft" section now, and it includes instructions for several ornaments like the one shown here. Note that the templates are blank (without images). This allows you to add your own clipart (in case you wanted a Santa-themed ornament, or a snow-themed ornament instead of a religious-themed ornament).

And you don't need clipart at all; I printed out some blank ones and my kids loved drawing their own pictures on them.

We have the following ornament templates/instructions:

• Cube ornament
• Dodecahedron ornament
• Icosahedron ornament

The cube is a good size to put on a tree; the other two are too large for a tree. The dodecahedron was designed as a table-top ornament, and the icosahedron as an ornament to hang from the ceiling or doorway frame.

In addition to the ornaments, there are several tutorials, in case you are interested in designing your own projects, such as the partially complete cathedral shown here.

Happy crafting, and Merry Christmas!

Good morning, and happy 3rd day of Christmas. I don't have any French hens for you, but I do have a bit of a Christmas puzzle for you to work out. The first person to submit a 100% correct solution will win a Pro Membership on the site, which gives you access to many features that aren't publicly available (like creating your own mazes, interactive word games, and more).

So here's the puzzle. Every year we fill stockings on Christmas Eve. This year I had a problem - one of the items for my wife's stocking was too big to fit in the stocking. So I wrote instructions for where she was supposed to find the gift. But I didn't put the instructions in her stocking. Oh no, that would be far too easy. I cut the instructions up into six pieces (being careful to cut them in such a way that it would be difficult to interpret the instructions if even one piece was missing) and hid them in various places around the house.

Then I created five rebus puzzles, which - when solved - gave the clues to where the puzzle pieces were located. The rebus puzzles were then taped to various items in her stocking, so she would discover them one at a time as she unloaded her loot.

The rebus puzzles are below. Before trying to solve them, you should know that they are all references to items that are in our home. One of them is an item that is only in our home around Christmas time. Most of them are items that are in everyone's homes.  One item, I will tell you, is a map hanging on our wall. So to solve that rebus, you have to be able to tell me the location shown in the map. Another puzzle might require a google search.

Click on any picture to get a bigger version. When you think you know all six objects, click the "Ask your question" link at the top of bottom of the page to submit your answer. Once someone has solved all the puzzles, I'll post a note to that effect in this blog post. Sometime in January I will post the solutions to the rebus puzzles. Merry Christmas!

And by the way, if you enjoy rebus puzzles, there are books available on Amazon that have hundreds of these puzzles! Here's one that has over a thousand rebus puzzles:

I love books. I especially love books that are beautiful. And I adore books that make a positive difference in the world. If you're looking for gift ideas this Christmas, I highly recommend that you pick up one - or even more - of these to give to friends and family.

I won't give a full book review, because Book Scrounger has already provided a review. I'll just say that a portion of the proceeds from this book are making a difference in the lives of people displaced from their homes due to war. Simply by purchasing the book, you are making a difference to people in need. Make sure you pop over to Book Scrounger to read the full review of Stepping Stones.

Or you can purchase it here: Purchase Stepping Stones.

Speaking of Book Scrounger, I think she likes books even more than I do - she has a whole blog dedicated to them. And starting December 1st, she'll be posting a Christmas Countdown - one Christmas book every day until Christmas!

So if you're looking for more Christmas gift ideas, click the image below to see the list as it progresses through the month. Be sure to bookmark the page, so you can go back to it each day for a new book recommendation!

Merry Christmas from me and my four year old son. Here's a Christmas tree ornament we built this morning. Each face is a triangle, and there are twenty faces in all. The faces are all made from last year's Christmas cards, cut into circles, and then folded around the shape of an equilateral triangle, in order to simultaneously form the face and provide a surface for gluing. Click the image for a larger view.

The icosahedron is one of 5 Platonic solids (regular solids). The complete list is:

• Tetrahedron: Four sides that are all equilateral triangles
• Cube: Six sides that are all squares
• Octahedron: Eight sides that are all equilateral triangles
• Dodecahedron: Twelve sides that are all regular pentagons
• Icosahedron: Twenty sides that are all equilateral triangles

I've made ornaments/decorations from three of those five shapes; maybe when I've done all five I'll publish an instruction sheet for each!

Merry Christmas! 

I was up at 3:30 AM today, so I decided to create a Christmas graph for all of my friends. This graph is made up of several inequalities combined with  ∩ (intersection) and  ∪ (union), and I hope you'll stick with me to the end to see what it looks like. Are you ready?

Let B be the equation: y² + 0.5y ≤ 0; {-0.5 ≤ x ≤ 0.5}

Let S be the equation: 81x⁴ - 18x²y² + 153x²y -326.25x² + y⁴ - 17y³ + 108.25y² - 306y + 324 ≥ 0 {-1/12 ≤ x ≤ 1/12}

Let C₁ be the equation: (x - 0.3)² + (y - 2.5)^2 - 0.0625 ≤ 0

Let T be the equation: 4x²y - y³ + 8y² - 16y ≤ 0

Let C₂ be the equation: x² + y² - 3y - 4 ≤ 0

Let O be the equation: [(x - .3)² + (y - 2.5)² - 0.02][(x - .3)² + (y - 2.5)² - 0.02][(x - .3)² + (y - 2.5)² - 0.02] ≥ 0

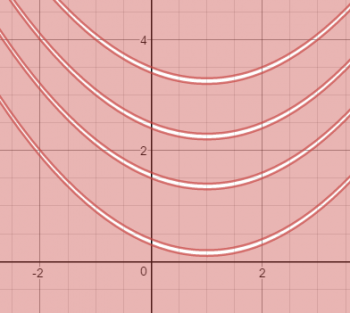
Let G be the equation: (y - .1 - .2(x - 1)²)(y - .2 - .2(x - 1)²)(y - 1.3 - .2(x - 1)²)(y - 1.4 - .2(x - 1)²)(y - 2.2 - .2(x - 1)²)(y - 2.3 - .2(x - 1)²)(y - 3.2 - .2(x - 1)²)(y - 3.3 - .2(x - 1)²) ≥ 0

Now graph the following:

B ∪ (S ∩ C₁) ∪ (T ∩ C₂ ∩ O ∩ G)

Okay, okay, this thing is ugly. I'm going to make it a little less ugly by factoring S, B, and T for you. You should be able to factor B and T on your own, but I'm certainly not going to ask anyone to factor S, so I'll just tell you how it factors. If you want to factor B and T on your own, take a moment to do so before reading further.

S factors into: (3x + y - 4.5)(3x - y + 4.5)(3x - y + 4)(3x + y -4) ≥ 0 {-1/12 ≤ x ≤ 1/12}

B factors into y(y + 0.5) ≤ 0; {-0.5 ≤ x ≤ 0.5}

T factors into:  y(2x + y - 4)(2x - y + 4) ≤ 0 (see the factoring process)

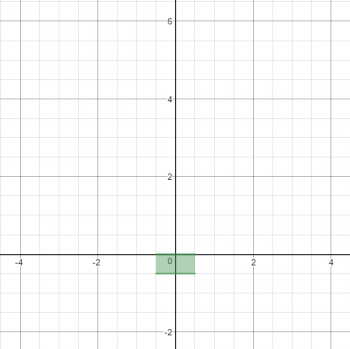
Let's begin by graphing the easiest part of this: B.

Since y(y + 0.5) ≤ 0, we can conclude that y must be between 0 and -0.5, so that the product of the two factors will be less than 0. However, we are also given the stipulation that x is between -0.5 and +0.5, which results in a simple box.

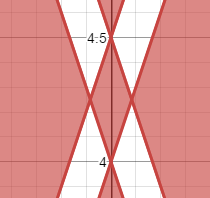
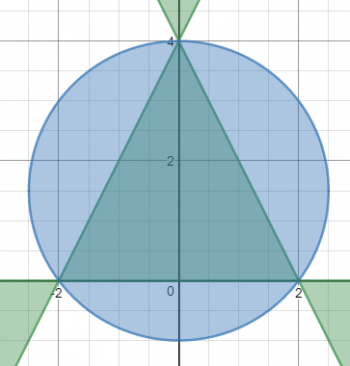
Now let's take a look at the intersection of S and C_1. S is a multiplication of four factors which are all linear, and they are in parallel pairs, which means this is going to be a parallelogram. Inside the parallelogram, two of the factors are negative and two are positive, which makes the whole thing positive. The graph looks like the picture to the right.

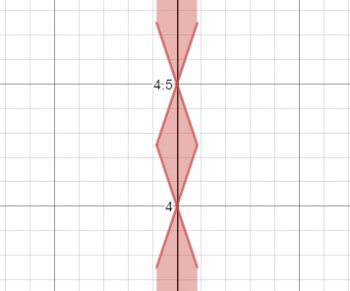
However, we have placed restrictions on the domain of this equation; x has to be between -0.5 and +05, which limits the graph as shown at the right.

We still are not finished with this section of the graph; we have to intersect this with the equation C₁. This graph is a circle with center at (0, 4.25), and the interior of the circle is included. This further limits the graph to nothing but the rhombus.

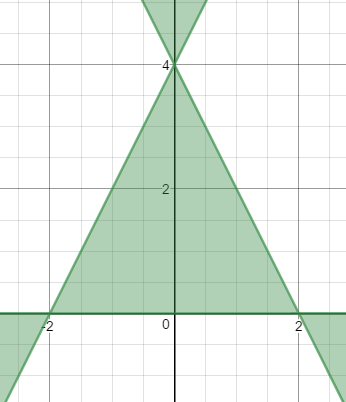
Okay, now the really challenging part. Equation T is very similar to equation S, except that instead of four factors, there are three. Thus, this contains a triangle, and since there are an odd number of factors, and they multiply to something less than or equal to zero, the interior of the triangle is included.

What's next? Well, in case you hadn't guessed C₂ is also a circle, and we're intersecting the interior of the circle with the triangle graph, which gives us the next graph.

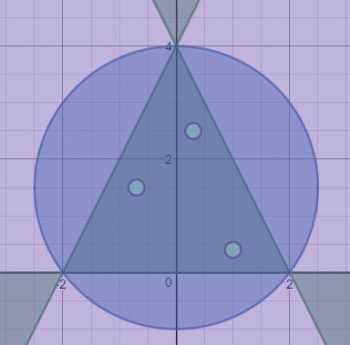
Then we have to deal with that hideous equation O, which appears to be...three circle factors multiplied together. If a point is on the interior of any of those three circles, that factor will be negative, and the other two will be positive, giving a negative result. However, equation O has the product greater than or equal to zero, which means that points satisfying O lie on or outside the three circles. The circles are all pretty small, and they're scattered around inside the triangle. Thus, we have the interior of a triangle, minus three circles, giving us the graph shown here.

What next? The even uglier equation G, which is a series of parabolas multiplied together as shown here.

Now, if you were to take all of these and overlay them on top of one another, they would look something like this:

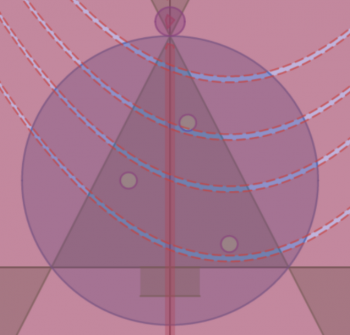
But...we're not overlaying them all; we have to take the intersection of T, C₂, O and G, and we also have to take the intersection of S and C₁. Then we overlay them (because it is a union of three separate graphs). I've shown them here with distinct colors for each of the three parts combined. Brown for the base (B), green for the tree (Tree ∩ Circle₂ ∩ Ornaments ∩  Garland), and yellow for the star (Star ∩ Circle₁).

Have a wonderful, Merry Christmas!
Professor Puzzler

P.S. Graph screen captures came from this graphing calculator.