Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
From Amber: "I'm trying to figure out the angle of a set of stairs using a scalene triangle basically you have a 90 degree angle one side is 8 feet and one is 3.5 feet what would be the slope or the angle of the third side"
Hi Amber. You didn't state in your question whether 8 feet is the horizontal length of the staircase and 3.5 feet the height? Or perhaps 8 is the length along the slope of the staircase? Of course, that makes a difference, so I'll help you work it out both ways.
First, as you pointed out, you have a right triangle. If the 8 and 3.5 are the legs of the triangle, that's all you need.
However, if 8 is the hypotenuse, you need to use the Pythagorean Theorem to find the missing side length: x2 = 82 - 3.52. Which leads to x = 7.2 (approximately)
There are two basic rules that you need to know. The first rule is that the slope is "rise over run." In other words, it's the amount that the staircase rises divided by the amount the staircase goes horizontally. So if the staircase is 8 feet horizontally and 3.5 feet vertically, the slope is 3.5 / 8 = 0.4375. On the other hand, if the horizontal length is 7.2, the slope is 3.5 / 7.2 = 0.4861.
Okay, so now you need the second rule, which is that the slope is the slope is the same as the tangent of the angle. Or, to put it a little differently, the angle is the inverse tangent of the slope.
You probably know how to do trig functions on your calculator, but in case you don't, on most calculators, you'll get the inverse tangent function by pressing "2nd" (or "Shift") and then the "TAN" button. So you'll press 2nd TAN 0.4375 = 23.6 degrees. Or, if we're using the second possibility, 2nd TAN 0.4861 = 25.9 degrees.
In either case, that's a fairly shallow angle for stairs; I think the "standard" (at least in the US) is closer to 30 degrees than 25 degrees.
Hopefully that helps out - thanks for asking!

Sandy asks, "Why do onions make you cry and how do you stop it?"
Hi Sandy, are you familiar with the acronym VOC? VOC stands for "volatile organic compound." People are getting more and more familiar with the acroynym VOC, because people who are concerned about health and allergic reactions try to avoid VOCs. For example, if I'm in a house that has been recently painted, my throat will start to close up a bit, my whole mouth will start to itch like crazy, and I'll start to sound like Darth Vader when I'm breathing. The culprit? VOCs in the paint. So when we painted our new house, I had to look for low-VOC or VOC-free paints. And when the school where I teach was being painted, I had to let them know that they had to choose between me and paint with VOCs.
My point? You might be surprised to know that onions contain VOCs. We tend to think of VOCs as artificially produced chemicals that are used as additives, but VOCs also occur naturally. After all, the "O" in in VOC stands for "organic" so it does make sense that we'd find these chemicals in nature. So what exactly is a VOC? It's any organic compound that emits as a gas. VOCs are found everywhere - perfumes, gasoline, fuel oil, deodorants, shampoos, paints, candles, laundry detergents and fabric softeners...the list goes on and on. What do all of these have in common? You can smell them. That's a pretty good rule of thumb; if it has a fragrance, there's a good chance it has VOCs, because fragrances are carried on the gases emitted.
So, yes, onions have VOCs. The particular compound that causes crying is syn-Propanethial S-oxide (C3H6OS), which is called an organosulfur compound, because it is an organic compound containing sulfur. What does it do? It irritates the glands that produce tears.
Now, to answer the second part of your question, I want you to think about a puddle of water. Eventually that puddle will all evaporate, right? But what conditions will make that puddle evaporate more quickly? The higher the temperature, the more quickly the water will turn to gas (that's what evaporation is). The same reasoning works for VOCs - higher concentrations of VOCs will be emitted at higher temperatures. Therefore, if you want to cry less, stick the onion in the fridge (maybe even the freezer) for a while, until the entire onion is at much cooler temperatures. Then when you're ready to cut it, take it out and cut it immediately, before it has a chance to warm back up again. The release of the tear-inducing compound will be lessened.
And if that doesn't take care of the problem? Some people wear goggles while cutting onions!
Question from Federico: "How do you rationalize the denominator of a fraction if there are three radicals added together, like SQR(2) + SQR(3) + SQR(5)?"
That's an interesting question, and to be completely honest, it's not one I remember coming across before. So I had to play around with it to see what I could find out. I lucked out, though, and the first thing I tried seemed to work out pretty well.
I started out by using variables instead of numbers, to see if I could find something that would always work. I'll show you the work I did below.
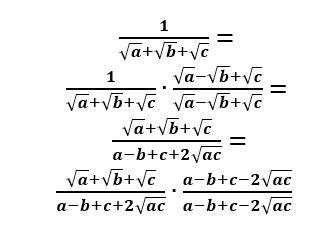
So what did I do? I replaced one of the plus signs with a minus, and multiplied numerator and denomator by that, similar to how we would multiply by the conjugate if there were just two terms. This caused all the radicals to disappear except the square root of ac, and that brings us to our normal simplification process.
So here's how it looks with your particular example:
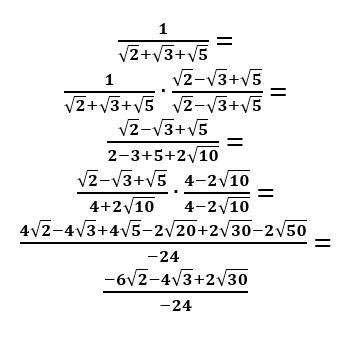
You can check on a calculator to see that the original value and my final "rationalized" value are the same thing.
Really, though, it doesn't look any simpler, and it was probably more effort than it was worth - but at least I know how to do it now - thanks for asking!
NOTE: I was so focused on rationalizing the denominator that I didn't even think about simplifying further. Of course, you know how to do that, and can finish the process for me!
7th grader Meera from U.A.E. asks the following question: "why should you use significant digits?"
Good morning Meera. This is an excellent question. I remember way back when I was in school, learning about significant figures and thinking, "This is a waste of time to try to keep track of how many digits I should use. It's a hassle, and who really cares how many digits I put in my answer?"
Of course, even back then, I was much more interested in theoretical instead of practical math and science. If you're anything like me, you'd rather give an exact answer like 22/3 or 5√2 instead of converting that to 7.333.. or 7.071068... and then figuring out how many decimals you're allowed to use.
Really, though, significant figures are the intersection of the theoretical and the practical. If all you were ever going to do is theoretical science, you would probably leave your answers in exact fractional or radical form, and never worry about significant figures. But practical science (engineering) requires you to use significant figures. Choosing not to do sig figs can be costly. Let me give you an example.
Suppose I contract a machine shop to build for me a cylindrical container that is 850 cubic cm in volume, and has a base area of 120 square cm.
Can you figure out how tall that cylinder would have to be? As a fraction it's 850 / 120, or 85 / 12 cm. But that's not helpful; who has tape measures marked to the nearest 12th of a centimeter? So they'll have to convert that to a decimal: 7.08333...
Which is still impractical, because who has a tape measure with infinite precision? Hmmm...what to do? They're going to have to round that number. And who decides how they round it? They do! So maybe they say, "Ah, 7.08333... is pretty close to 7, so we'll call that 7 cm."
So they build my cylinder, and now, instead of having a container with 850 cubic cm of volume, it has 7(120) = 840 cubic cm of volume. Not a big deal? Maybe. But maybe I actually have a reason that I want my container to hold 850 cubic cm of something, and now it's going to overflow because he didn't make it tall enough. So I bring it home, start filling it up, and whatever I pour into it (hopefully not sulfuric acid!) starts going all over the floor, because the container isn't actually as big as I wanted it. So now I have to go back to the machine shop and tell them they built it wrong, and they have to start over. That's going to cost someone - either me, or or the machine shop, depending on whether one of us can convince the other that it's their fault.
Here's where significant figures are important. Significant figures take all the guesswork out of how the machine shop should round. They should have looked at the two measurements I gave them (120 and 850) and said, "Each of these has two significant figures, therefore, the result of the division will have two significant digits. Thus, instead of rounding to 7 (one sig fig) we should round to 7.1 cm."
Now, if my cylinder is not the right size, they can point at the measurements I gave them and say, "We performed this exactly to your specifications, using the rules of significant figures."
What it boils down to is this: using significant figures is a way of indicated how precisely our quantities are known, or have been measured. Significant figures keep us from claiming more accuracy than we really have, and they're a way of communicating more precisely what we want. If I said said to the machine shop, "I want my cylinder to have a volume of 850.0 cubic cm, and a base area of 121 square cm," they would know that they need to be much more precise, and the result needs to have three significant figures: 7.08 cm.
I love books. I especially love books that are beautiful. And I adore books that make a positive difference in the world. If you're looking for gift ideas this Christmas, I highly recommend that you pick up one - or even more - of these to give to friends and family.

I won't give a full book review, because Book Scrounger has already provided a review. I'll just say that a portion of the proceeds from this book are making a difference in the lives of people displaced from their homes due to war. Simply by purchasing the book, you are making a difference to people in need. Make sure you pop over to Book Scrounger to read the full review of Stepping Stones.
Or you can purchase it here: Purchase Stepping Stones.
Speaking of Book Scrounger, I think she likes books even more than I do - she has a whole blog dedicated to them. And starting December 1st, she'll be posting a Christmas Countdown - one Christmas book every day until Christmas!
So if you're looking for more Christmas gift ideas, click the image below to see the list as it progresses through the month. Be sure to bookmark the page, so you can go back to it each day for a new book recommendation!



