What is the "altitude to the hypotenuse," and how do I find its length, if I know the lengths of two legs?

To answer this question, consider the diagram below. I show a triangle with angles A, B, and C, and right angle at C. The segment CD is the altitude to the hypotenuse. An altitude is a line segment that is perpendicular to a side, and passes through the opposite vertex. Thus, the altitude to the hypotenuse is perpendicular to the hypotenuse, and passes through the point C.

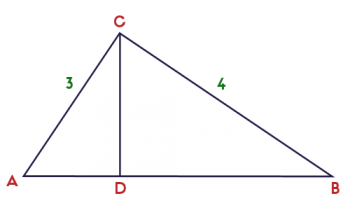
For this example, I gave the legs lengths 3 and 4. I did this so it would work out simply: the hypotenuse is 5 (because 3² + 4² = 5²).

The question is, how do we find the length of CD? To figure this out, it is helpful to notice that all three triangles are similar. 

ΔABC ~ ΔACD ~ ΔCBD 

From this, we know that the ratio of the longer leg to the hypotenuse is the same for each triangle.

In the largest triangle, that ratio is 4/5.  In the smallest triangle, that ratio is CD/3.

Thus, 4/5 = CD/3, which leads to CD = 12/5.

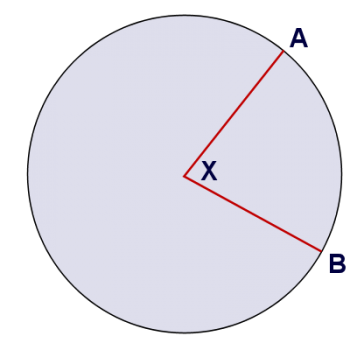
One student asks for an explanation of central angles - how is a central angle different from an inscribed angle?

The best answer to this question is probably a picture (or, rather, a pair of pictures). The first picture shows a circle with center at X. The angle has its center at the center of the circle. Therefore, it's a central angle.

The second picture shows an additional angle, marked in green. This angle is an inscribed angle, because its vertex lies on the circle.

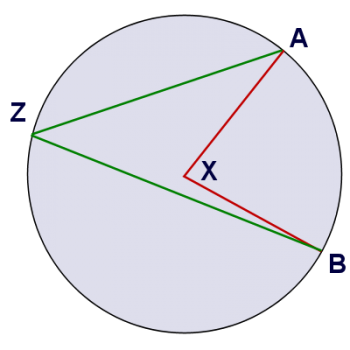
In both cases, the angles cut off the same arc - arc AB. So how are these two angles different? Well, if you look at the picture, you can see pretty easily that an inscribed angle is smaller than a central angle that cuts off the same arc. I think we can prove that the inscribed angle is half the size of the central angle. Want to give it a try?

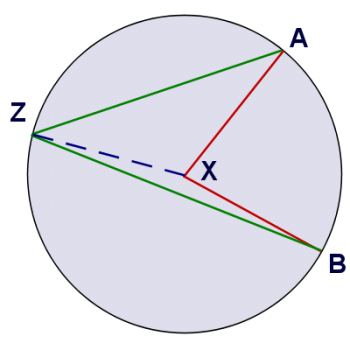
Let's construct a segment from Z to X, which splits the quadrilateral AXBZ into two triangles: AZX and BZX. Both of these triangles are isosceles (because two of their sides are radii of the circle). If we let m be the measure of angle AZX, n be the measure of angle BZX, and k be the measure of the central angle, then we can write the following equation for the sum of all the interior angles of the quadrilateral AXBZ:

(measure of AZB) + (measure of B) + (measure of A) + (measure of X) = 360

(m + n) + (n) + (m) + (360 - k) = 360

2m + 2n + 360 - k = 360

k = 2(m + n)

And since m + n is the measure of AZB, we've shown that the measure of a central angle has twice the measure of any inscribed angle that cuts the same arc. I hope that's helpful!

9th grader Akhil from Kerala asks the following: "The sides of a quadrilateral are extended to form exterior angles. Find the sum of these exterior angles."

Hi Akhil, instead of just answering the question you asked, I'd like to explore the question in a little more depth, and explain why the answer is what it is. After all, if I just told you the answer, that would make for a pretty boring blog post!

So let's start off with a quadrilateral. I'm going to show you a picture of one below, and ask a question about it. How many degrees are there in the measures of all the interior angles of the quadrilateral?

Now, you might already know the answer to that question; the sum of all the interior angles is 360 degrees. But can you prove that to be true? It's actually not hard to understand why that quadrilateral (and all quadrilaterals, for that matter) have an interior angle sum of 360 degrees. To see why, just look at this picture, in which I've divided the quadrilateral into triangles:

How many triangles did it take to divide up that quadrilateral? It took two, right? And how many degrees does each of those triangles have? 180 degrees. And so altogether, how many degrees do they have in total? 180 x 2 = 360 degrees.

Understanding that the total of the interior angles is 360 degrees is important to finding the number of degrees in the exterior angles. Here's a picture that shows what you described - the sides being extended to form exterior angles:

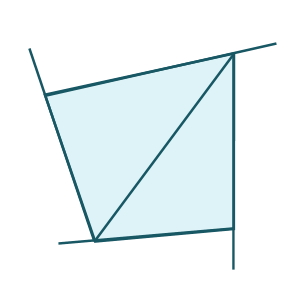
By extending these sides, we've created linear pairs - pairs of angles that form a straight line. Each linear pair includes an interior angle and an exterior angle. Each linear pair adds to 180 degrees (a straight line), and there are four linear pairs (because there are four sides).

So if there are 4 linear pairs, and each linear pair is 180 degrees, that's a total of 720 degrees. But 360 degrees of that is interior angles, so the exterior angles have to add up to 720 - 360 = 360 degrees! And that's your answer.

Now, it might be tempting to think that the interior angles of a polygon and the exterior angles of a polygon will always match, since they do in the case of a quadrilateral, but that is not the case. Let's take a look at a pentagon to see why. Here I'll give you a pentagon divided into triangles, and with sides extended:

In the case of a pentagon, we can divide the polygon into 3 triangles, which means the interior angles add to 3 x 180 = 540 degrees.

We've created 5 linear pairs, which total 5 x 180 = 900 degrees.

Since there are 900 degrees total, and the interior angles add to 540 degrees, the sum of the exterior angles is 900 - 540 = 360 degrees!

It turns out that the sum of the exterior angles is 360 degrees regardless of whether it's a quadrilateral or a pentagon.

What do you think...can you generalize it even further? How many degrees are there in the interior of an n-gon? And how many degrees in the exterior angles of an n-gon? I'll leave it to you to figure that out. Thanks for asking, Akhil!

Fourth grader Alice asks, "How many diagonals are in decagon?"

Great question, Alice. But instead of giving you an answer to that question, I'm going to show you how you can figure it out for yourself. And not only that, I'll show you how you can figure out the answer for any polygon, even if it has 20, or 50, or 2000 sides!

Ready? Let's start with a simple example. We'll go with a polygon that has 8 sides (which is called an octagon), like this:

Now, this polygon, because it has eight sides, also has eight vertices. It seems a bit overwhelming to try to figure out all the diagonals, so let's just focus on one vertex. How many diagonals can you draw in an octagon, that all begin at one vertex?

The answer to that question is five. Take a look at the diagram below:

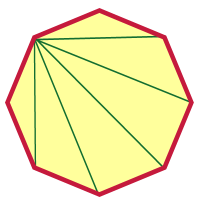
In this diagram I've chosen the diagonal to the left just below the top vertex, and I've drawn diagonals to every vertex that I can draw a diagonal to. Which diagonals can't I draw diagonals to? Well, I can't draw a diagonal from a vertex back to itself, and I can't draw diagonals to the two vertices next to that one (because those wouldn't be diagonals; they'd be sides!).

So there are three vertices I can't draw diagonals to from that vertex. Eight vertices total, minus the three I can't draw to, leaves five. That's important to remember: subtract 3 from the number of vertices, and you have the number of diagonals you can draw from any vertex.

But that's just one vertex! You could draw diagonals from any vertex, right? Sure! And there are eight vertices in our octagon, so we take the number of diagonals per vertex, and multiply it by the number of vertices: 5 x 8 = 40.

You might be tempted to think that that's our answer, but it's not. Why not? Because we've counted every diagonal twice! Every diagonal has two vertices, so we've counted it from one end, and we've also counted it from the other end. So to get the actual number of diagonals, we have to divide our answer by 2. 40 / 2 = 20. There are twenty diagonals in an octagon.

Let's try that reasoning on a polygon that has 2000 sides. Now, I'm not going to draw a 2000-gon for you; we'll just have to work out the reasoning without a picture.

1. Pick a vertex. How many diagonals can you draw from that vertex? Answer: 2000 - 3 = 1997.
2. How many vertices total? Answer: 2000
3. How many diagonals counted from all the vertices? Answer: 1997 x 2000 = 3,994,000
4. Oops! We've counted each diagonal twice! How do we get rid of the duplicates? Answer: 3994000 / 2 = 1,997,000

So a 2000-gon has 1,997,000 diagonals!

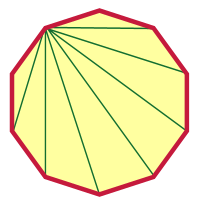
After doing something as crazy as a 2000-gon, a decagon shouldn't seem so difficult, right? I'll get you started, and you can finish it from here. I picked a vertex and drew diagonals from that vertex.

How many are there? Were you able to figure out how many there were without looking at the picture?

Can you figure it out from here? I hope so! Good luck, Alice. 

By the way, there is a formula you can use; it looks like this: D = n(n - 3)/2. But honestly, I don't expect my students to memorize it. I expect them to remember how we reason it out here. If you understand the logic, it's even better than having a formula!

Seventh grader Colton from Florida asks, "If triangles have the same area, are they similar? Or do triangles have to have the same perimeter to be the same? I think it's area. Thank you "

Hi Colton! 

Thanks for your question. I want to make sure we're talking about the same thing here. In one question you talk about triangles being "similar" and in the next you talk about them being "the same." These are two very different questions, that use very different concepts.

You see, triangles could be congruent (what you might have meant when you said "the same") or they can be similar.

So what is the difference?

Congruent means that two triangles are identically shaped. The have the same shape and the same size.  They have three pairs of sides that are the same length, and they have three pairs of angles that are the same measure. We call the pairs of parts "corresponding parts," and we say that in congruent triangles, "Corresponding parts of congruent triangles are congruent" (which gets shortened, often, to "CPCTC").

Another way of saying that: if you have two triangles that are congruent, you could pick one of them up and set it down on top of the other, and they would match perfectly. You might have to flip or rotate the one you picked up, but if you can't make it line up perfectly on the other triangle, they aren't congruent. In the image below, the triangles are congruent, because you could pick up the one on the right, rotate it about 45 degrees counter clockwise, and it would fit exactly on top of the triangle on the right.

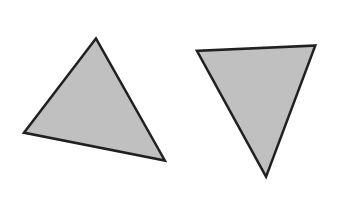
As for your question: if two triangles have the same area, are they congruent? Not necessarily! I can create two triangles that take up the same amount of space, but have very different shapes. And the same is true of perimeter; just because two triangles have the same perimeter, that doesn't mean they're the same shape.

There are ways to tell if two triangles are congruent. For example, if you have two pairs of sides that are the same length, and the pair of angles between those sides is congruent, then it's guaranteed that the two triangles are congruent. Maybe in another blog post I'll explore all the different congruence theorems!

But now we need to consider similarity. Similarity is different from congruence. Two triangles can be similar without being congruent. Two triangles are similar if they have the same shape, but not necessarily the same size. What do I mean by "same shape?" Well, one way of explaining it is to say that all of their pairs of angles are congruent. 

Or, imagine that you have two similar triangles printed on transparencies. You might not be able to lay one on top of the other so that they match, but if you hung one of them on the wall, and used a projector to project the other one onto the wall, you could make them line up by getting the projector the right distance from the wall.

This picture is an example of two triangles that are similar. You can see the shape is the same; they both have two smallish angles, and one bigger angle. You couldn't lay one of them on top of the other and have them match perfectly, but if you expanded the smaller one, you could make it fit perfectly on the larger one. They are similar.

Okay, so now we come back to your question: if two triangles have the same area, or the same perimeter, are they similar? Not necessarily! You could have two triangles with the same perimeter (or the same area) that aren't the same shape at all. And if they're not the same shape, they're not similar!

So, in conclusion, neither the area nor the perimeter will help you determine if two triangles are similar, or determine if they are congruent!

That's a pretty long answer to a short question, but hopefully you learned some important concepts along the way.

Thanks for asking your question, Colton.

Sincerely,
Professor Puzzler